Um carro percorre uma estrada que passa por uma colina cujo formato, no trecho próximo do alto, é praticamente circular, como indicado na figura, em que o ponto C corresponde ao centro do círculo de raio R = 90 m.
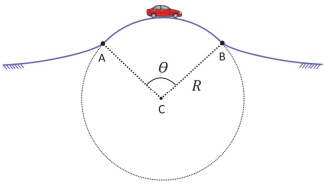
a) No ponto mais alto da trajetória, a motorista do carro em movimento sente-se “mais leve” do que se estivesse sentada em um carro parado. Nessas condições, o módulo da força normal, N, sobre a motorista é maior, menor ou igual ao módulo de seu peso, P? Justifique a sua resposta.
b) Calcule o tempo Δt necessário para que o carro percorra a distância entre os pontos A e B, indicados no desenho, supondo que sua velocidade tenha módulo constante e igual a 72 km/h e que o ângulo θ seja igual a 2 radianos.
c) Calcule a máxima velocidade que o carro pode ter para que, no ponto mais alto da colina, não perca o contato com a pista.
Note e adote:
Aceleração da gravidade: g = 10 m/s2.
a) No ponto mais alto da trajetória, cujo formato é praticamente circular, a normal e o peso
têm mesma direção (vertical) e sentido opostos, como ilustrado na figura seguinte.
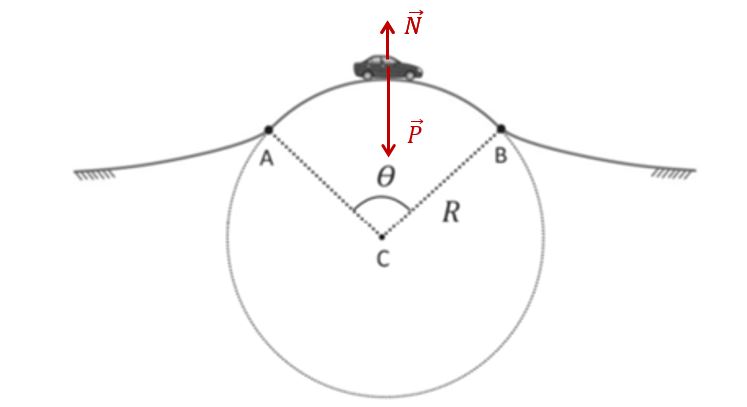
Nesse ponto, a resultante das forças aplicadas no automóvel possui uma componente centrípeta, uma vez que o formato da trajetória é circular. Sendo assim, a normal , que aponta para fora do centro da curva, é menos intensa que o peso
, que aponta para o centro da curva.
b) O deslocamento do carro ΔS entre os pontos A e B pode ser determinado a partir definição de radiano, como segue:
Substituindo-se os dados numéricos fornecidos:
Logo, o intervalo de tempo para que o carro percorra essa distância a uma velocidade v = 72 km/h = 20 m/s pode ser determinado pela definição de velocidade média, da seguinte maneira:
c) A relação entre a intensidade da normal no ponto mais alto da trajetória e a velocidade v do carro nesse ponto pode ser obtida por meio da 2ª lei de Newton para movimentos circulares:
Logo, quanto maior for a velocidade do carro, menor a intensidade da normal. Dessa forma, a velocidade será máxima, quando a normal for nula:
Substituindo-se os dados numéricos fornecidos: