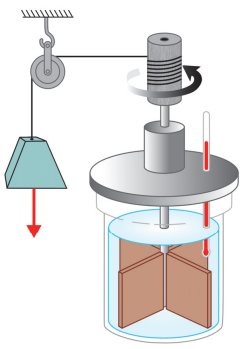
Em seu projeto para uma feira de ciências, uma estudante decide reproduzir o experimento histórico de Joule sobre o “equivalente mecânico do calor”. Ela então monta o aparato esquematizado na figura ao lado. No experimento, a estudante deixa cair um bloco preso a uma corda que passa por uma roldana e cujo movimento faz girar pás que agitam o líquido contido em um calorímetro termicamente isolado.
a) O bloco, de massa igual a 5 kg, cai com velocidade praticamente constante. Qual é a força de tração na corda?
b) Suponha que o bloco caia até o chão, partindo de uma altura de 50 cm. Entre o início e o final da queda, determine o trabalho mecânico realizado pela força peso sobre o bloco e a variação da energia potencial gravitacional do sistema formado pelo bloco e pela Terra.
c) Suponha agora que o bloco seja substituído por outro e que, durante a queda desse novo bloco, a força peso atuando sobre ele realize um trabalho de módulo igual a 70 J. Suponha ainda que o líquido no calorímetro tenha massa de 10 kg, que seu calor específico seja de 2000 J kg-1 K-1 e que o termômetro utilizado pela estudante tenha precisão de 0,1 K. A estudante conseguirá medir a variação de temperatura do líquido provocada pela queda do bloco? Justifique a sua resposta.
Note e adote:
Aceleração da gravidade: g = 10 m/s2.
Suponha que a corda seja inextensível e que a roldana tenha massa desprezível.
Despreze todos os atritos, exceto a resistência do líquido ao movimento das pás.
Despreze as dimensões do bloco.
a) Uma vez que a velocidade do bloco é constante, a sua resultante () é nula. A figura a seguir ilustra as forças aplicadas ao bloco.
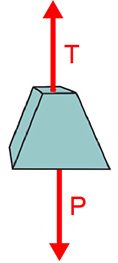
Assim sendo, para que a resultante seja igual a zero:
b) Como a força peso tem intensidade constante, o trabalho realizado por essa força é dado por:
Fazendo as devidas substituições numéricas para as grandezas com as unidades do Sistema Internacional:
A variação da energia potencial gravitacional (ΔEP) do sistema bloco/Terra é dada por:
Adotando como referência o solo (h = 0), segue que .
Assim, a variação de energia potencial gravitacional do sistema bloco/Terra é:
c) Supondo que a queda desse segundo bloco também ocorra com velocidade constante, e considerando que a única força resistiva é aquela que o líquido exerce sobre as pás, podemos assumir que a redução de energia potencial gravitacional do bloco (70 J) tenha sido compensada pela transformação dessa energia em energia térmica, responsável pelo aquecimento do líquido.
Nessas circunstâncias, para o líquido:
, em que Q = 70 J
Assim, procedendo as substituições numéricas:
Uma vez que a precisão do termômetro da estudante é de 0,1K, ela não conseguirá medir essa variação de temperatura.