A partir do recorte de um quadrado cujo lado mede 10 m, um artista plástico fez uma obra em metal representada na Figura 1, cuja planificação é mostrada na Figura 2.
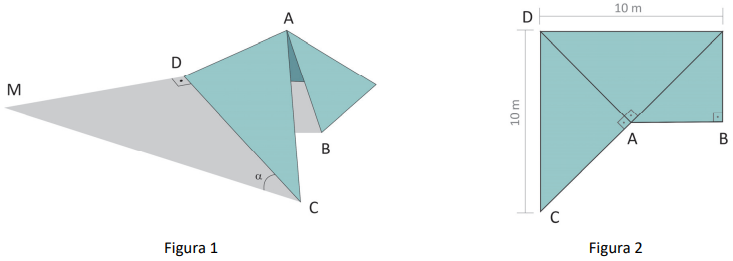
Observe as Figuras 1 e 2 para responder:
a) Supondo que a medida da área da sombra externa da escultura, representada pelo triângulo DMC, seja o dobro da medida da área do triângulo DAC, qual é a medida do ângulo α, indicado na Figura 1?
b) Supondo que a medida da área do triângulo DMC seja k vezes a medida da área do triângulo DAC, determine o valor de k em função de α.
c) Qual é a medida da projeção ortogonal do segmento AB no solo, supondo que o ângulo desse segmento em relação ao solo seja 60°?
Seja E o vértice superior direito do polígono representado na Figura 2. Note que é altura do triângulo isósceles CDE e, portanto, A é ponto médio do segmento
. Como o polígono ABEDC foi obtido a partir do recorte de um quadrado, tem-se que A é centro desse quadrado. Assim,
,
e
.
a) Denotando por e
as áreas dos triângulos DMC e DAC, respectivamente, e considerando as medidas dos segmentos em metros, temos:
Assim, o triângulo DMC é retângulo e isósceles e .
b) Analogamente, tem-se:
Assim, no triângulo retângulo DMC, tem-se:
Portanto, se a medida da área do triângulo DMC é k vezes a medida da área do triângulo DAC, tem-se .
c) Seja P a projeção ortogonal do ponto A no solo. Considere o triângulo ABP, representado na figura a seguir, onde é a projeção ortogonal do segmento AB no solo.
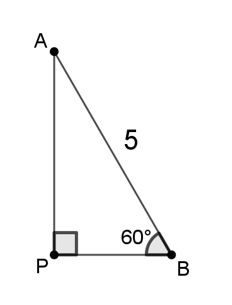
Neste triângulo:
Portanto, se o ângulo do segmento em relação ao solo é de 60°, a medida de sua projeção ortogonal no solo é
metros.