O centro do círculo branco indicado na figura divide a altura relativa à base do triângulo isósceles ABC, com AB=AC, em dois segmentos de reta: um de 5 cm e outro de 3 cm. Na figura há, ainda, um setor circular de centro A e arco
.
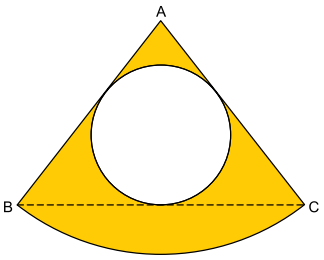
a) Calcule o perímetro do triângulo ABC, que circunscreve o círculo branco.
b) Adotando sen 53,13º = 0,8 e p = 3,14, calcule, em cm², a melhor aproximação inteira da medida da área da região indicada em amarelo na figura.
a) Observe a figura:
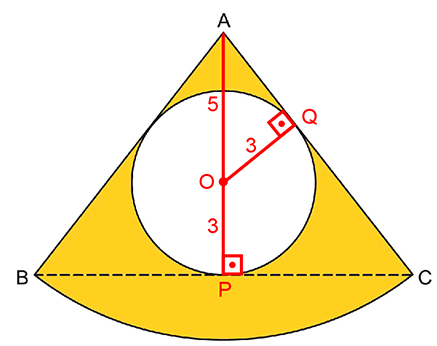
Aplicando o teorema de Pitágoras no triângulo retângulo AQO, vem e, portanto,
Da semelhança entre os triângulos APC e AQO, tem-se:
Aplicando o teorema de Pitágoras no triângulo APC, vem e, portanto,
Como , então
e, portanto, o perímetro do triângulo ABC vale
b) Do item anterior, tem-se o que implica que o ângulo
mede 53,13° e seu complemento
mede
A área pedida S pode ser obtida calculando a área do setor circular cujo raio mede 10 cm e ângulo central medindo subtraindo a área de um círculo de raio medindo 3 cm. Logo:
Usando tem-se que
cuja melhor aproximação inteira é igual a 36 cm².