A trave de equilíbrio é um aparelho de ginástica artística, no qual a atleta deve se equilibrar enquanto realiza movimentos coreográficos, saltos e giros. A Figura 1 representa a trave de equilíbrio. A trave é paralela ao solo e os pontos A, B, e C formam um triângulo equilátero. A Figura 2 representa um dos movimentos realizados pela atleta.
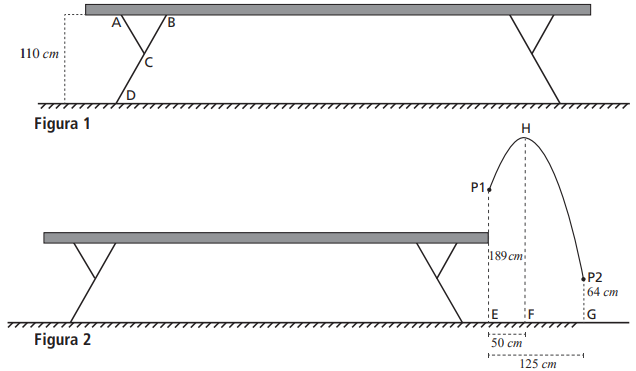
a) Sabendo que a distância da trave ao solo é de 110 cm, calcule o comprimento do segmento DB.
b) A atleta realiza um salto de saída da trave, representado na Figura 2. Sabe-se que a trajetória do centro de massa da atleta é uma parábola, conforme ilustrado na figura 2. A distância horizontal entre a saída da trave e o local da aterrisagem é 125 cm e o ponto mais alto da trajetória (ponto H) é alcançado a 50 cm da saída da trave (distância horizontal). Sabe-se que no momento da saída, o centro de massa está a 189 cm do chão (ponto P1) e que no momento da aterrisagem o centro de massa da atleta está situado a 64 cm do chão (ponto P2), como mostra a figura. Calcule a maior altura atingida pelo centro de massa da atleta durante esse movimento.
a) Dado que os pontos A, B e C formam um triângulo equilátero, tem-se que Com isso, tem-se a figura a seguir, em que
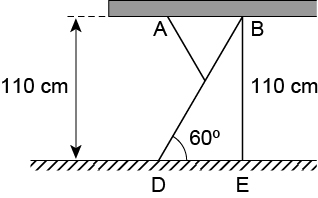
b) Considere a figura cotada a seguir:
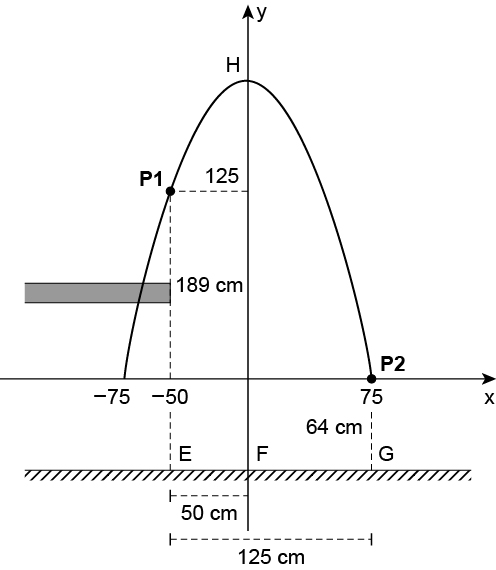
A equação da parábola representada na figura é
Como tem-se:
Logo,
Portanto, a maior altura atingida pelo centro de massa da atleta durante esse movimento é