Helena tem um cadeado cuja abertura depende de uma senha composta por 3 dígitos que são números inteiros de 0 a 9. Após definir a senha do cadeado, ela cola um adesivo com certo código no cadeado. Este código, no entanto, não é a senha do cadeado: deixar a senha anotada no cadeado seria um equívoco. Para obter a senha correta, (x,y,z), a partir do código (a,b,c), Helena usa a seguinte relação entre os dígitos do código e os dígitos da senha:
a) Se o código anotado por Helena fosse (9,6,3), qual seria a senha do cadeado?
b) Passados alguns meses, Helena se esqueceu da senha. Para seu azar, o adesivo com o código se apagou parcialmente e só sobraram visíveis os dois primeiros dígitos: (6,2,?). Quais são todas as possíveis senhas? Justifique.
a) Considerando o sistema , temos:
- Da 1ª e 2ª equações, pode-se concluir que y = 3;
- Da 1ª e 3ª equações, pode-se concluir que x = 6;
- Da 2ª equação e de x = 6, pode-se concluir que z = 0.
Logo, a solução do sistema é (6, 3, 0).
b) Consideremos o sistema . Dessas duas equações, conclui-se que
ou seja,
Sendo x e z números inteiros de 0 a 9 e conclui-se que
ou
Tem-se a seguinte tabela de valores possíveis:
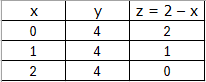
Portanto, as possíveis senhas são dadas por (0, 4, 2), (1, 4, 1) e (2, 4, 0).