Um designer de produtos deseja fabricar um vaso para flores conforme a figura a seguir.
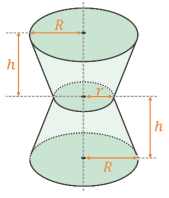
Sabe-se que a base e o topo do vaso são uma circunferência de raio R que mede 10 cm, a parte central é uma circunferência de raio r de 5 cm e a medida h mede 12 cm. Qual é a capacidade volumétrica desse vaso em cm3?
Considere a figura abaixo, na qual os segmentos tracejados são a continuação do tronco de cone inferior do vaso.
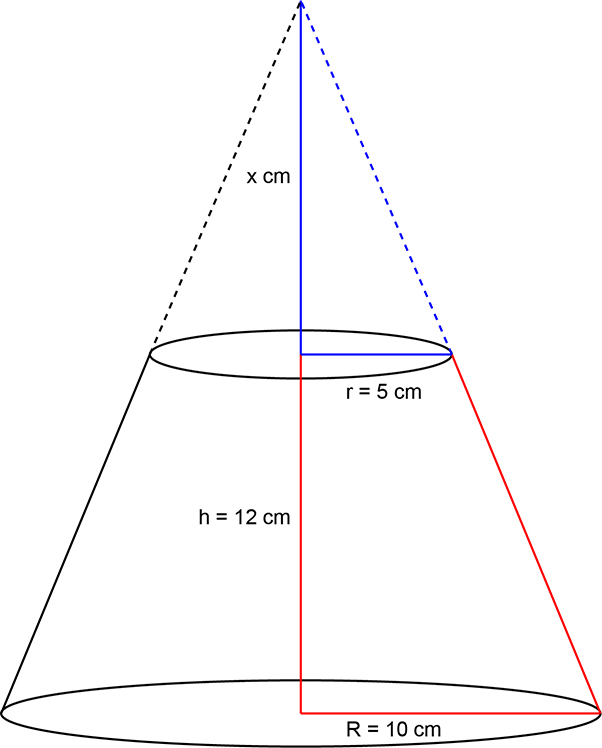
Por semelhança de triângulos, tem-se, em cm, que:
Considerando o cone maior como sendo o cone de raio 10 cm e o cone menor como sendo o cone de raio 5 cm, tem-se que a capacidade volumétrica do vaso (Vvaso), em cm3, será:
Então: