Um tanque, em formato de paralelepípedo reto retângulo, tem em seu interior dois anteparos verticais, fixados na sua base e em duas paredes opostas, sendo perpendiculares a elas, conforme a figura.
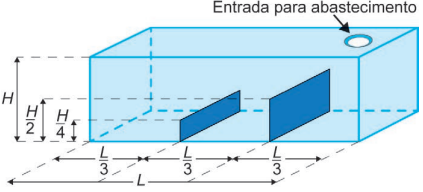
Esses anteparos, de espessuras desprezíveis, estão instalados de maneira a dividir a base do tanque em três retângulos congruentes, tendo suas alturas iguais à metade e a um quarto da altura do tanque. O tanque é abastecido por uma entrada situada no teto, através de um duto que despeja água a uma vazão constante, sendo necessárias 12 horas para finalizar o seu enchimento.
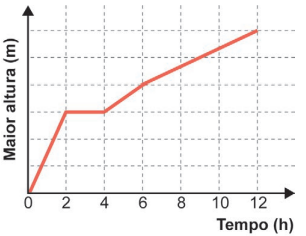
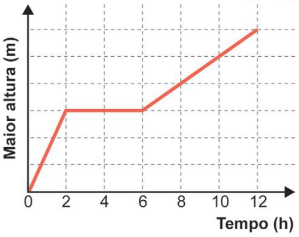
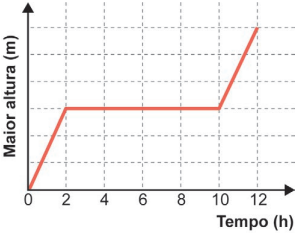
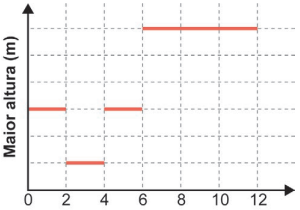
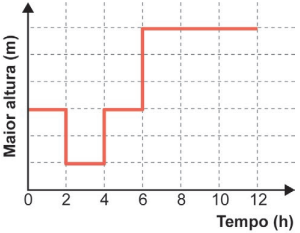
O gráfico que descreve, em cada instante, a maior altura de coluna de água, dentre aquelas que vão sendo formadas ao longo do enchimento do tanque, é
Vamos considerar que a água é despejada de modo a cair verticalmente sobre a base da região formada entre o segundo anteparo e a parede da direita.
Mantida a área da base de um paralelepípedo reto-retângulo, seu volume é proporcional à sua altura. Dessa forma, no início do preenchimento, a altura da água entre o segundo anteparo e a parede da direita aumenta constantemente, até chegar em . Com isso, podemos eliminar as alternativas D e E, que indicam um nível constante no início do processo.
Após atingir o nível máximo na porção mais à direita, a água começa a preencher o espaço entre os dois anteparos e, em seguida, o espaço entre a parede da esquerda e o primeiro anteparo, até que a água ocupe exatamente metade do reservatório, atingindo o nível em todos os pontos. Durante todo esse processo, o nível máximo da água permanece constante e igual a
.
Note que o volume total entre a parede da esquerda e o segundo anteparo é o dobro do volume entre o segundo anteparo e a parede da direita, de modo que o tempo em que o nível permanece constante e igual a é o dobro do tempo em que o nível cresce constantemente. Com essa observação, já podemos concluir que as alternativas A e C estão incorretas, o que nos leva à alternativa B.
Para confirmar que essa alternativa é, de fato, a correta, podemos pensar que, como a vazão é constante, o tempo levado para que todos os pontos atinjam o nível é o mesmo que o tempo levado para que a metade superior do reservatório seja completamente preenchida. No preenchimento dessa metade superior, o nível volta a crescer constantemente e, dado que o tempo total é de 12 horas, concluímos que são necessárias 6 horas para isso, como pode ser verificado na alternativa B.