A prefeitura de uma cidade planeja construir três postos de saúde. Esses postos devem ser construídos em locais equidistantes entre si e de forma que as distâncias desses três postos ao hospital dessa cidade sejam iguais. Foram conseguidos três locais para a construção dos postos de saúde que apresentam as características desejadas, e que distam 10 km entre si, conforme o esquema, no qual o ponto H representa o local onde está construído o hospital; os pontos P1, P2 e P3, os postos de saúde; e esses quatro pontos estão em um mesmo plano.
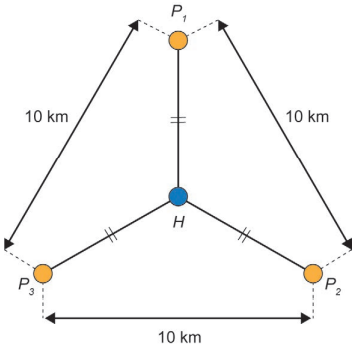
A distância, em quilômetro, entre o hospital e cada um dos postos de saúde, é um valor entre
Sendo a distância pedida, observe a figura a seguir, em que P1P2P3 é um triângulo equilátero com lados medindo 10 km e H é seu centro:
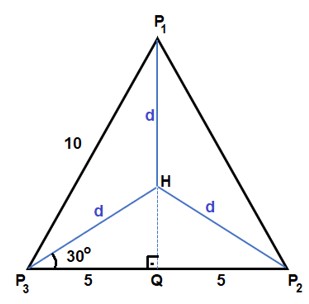
No triângulo retângulo HQP3, vem:
Como , então
e, portanto,
. Logo, a distância
é um valor entre 5 e 6.