Um aeroporto disponibiliza o serviço de transporte gratuito entre seus dois terminais utilizando os ônibus A e B, que partem simultaneamente, de hora em hora, de terminais diferentes. A distância entre os terminais é de 9000 metros, e o percurso total dos ônibus, de um terminal ao outro, é monitorado por um sistema de cinco câmeras que cobrem diferentes partes do trecho, conforme o esquema.
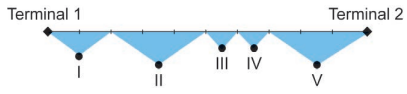
O alcance de cada uma das cinco câmeras é:
• câmera I: do percurso;
• câmera II: do percurso;
• câmera III: do percurso;
• câmera IV: do percurso;
• câmera V: do percurso.
Em determinado horário, o ônibus A parte do terminal 1 e realiza o percurso total com velocidade constante de 250 m/min; enquanto o ônibus B, que parte do terminal 2, realiza o percurso total com velocidade constante de 150 m/min.
Qual câmera registra o momento em que os ônibus A e B se encontram?
A distância que cada câmera alcança é:
Câmera I:
Câmera II:
Câmera III:
Câmera IV:
Câmera V:
As equações que descrevem a posição de cada ônibus são:
Ônibus A:
Ônibus B:
Para encontrarmos o momento do encontro, basta igualarmos as equações:
Agora basta substituir esse valor de t em umas das equações:
Como, até a câmera 3, cobrimos a distância de 1 800 + 2 700 + 900 = 5 400 metros, então a câmera que registrará o momento em que os ônibus se encontram é a câmera IV.