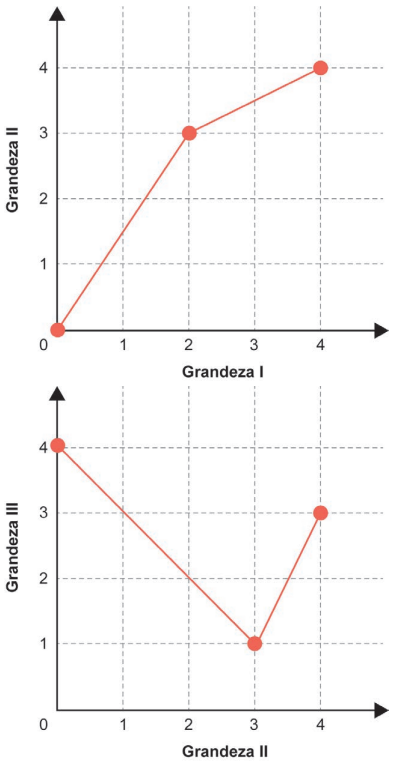
Três grandezas (I, II e III) se relacionam entre si. Os gráficos a seguir, formados por segmentos de reta, descrevem as relações de dependência existentes entre as grandezas I e II, e entre as grandezas II e III.
O valor máximo assumido pela grandeza III, quando a grandeza I varia de 1 a 3, é
Primeiramente analisando a relação de dependência das grandezas I e II, com a grandeza I variando de 1 a 3, tem-se a seguinte faixa do gráfico:
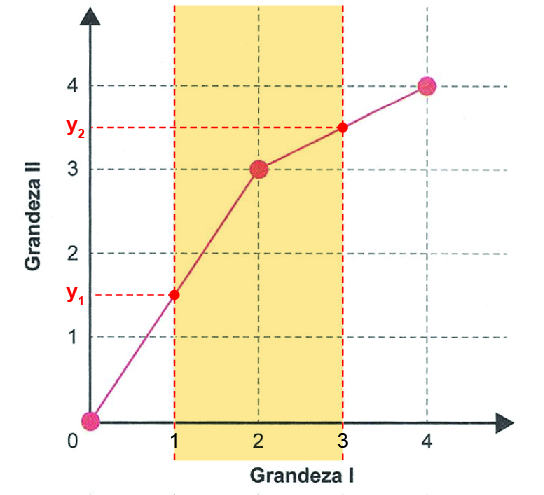 Para o trecho de 0 a 2, a partir dos pontos (0,0) e (2,3), conclui-se que a relação é expressa por
Para o trecho de 0 a 2, a partir dos pontos (0,0) e (2,3), conclui-se que a relação é expressa por e que, para x = 1 , obtém-se y1 = 1,5.
Para o trecho de 2 a 4, a partir dos pontos (2,3) e (4,4), conclui-se que a relação é expressa por e, para x = 3 , obtém-se y2 = 3,5.
Assim, quando a grandeza I varia de 1 a 3, a grandeza II varia de 1,5 a 3,5.
Agora, analisando a relação de dependência existente entre as grandezas II e III, tem-se:
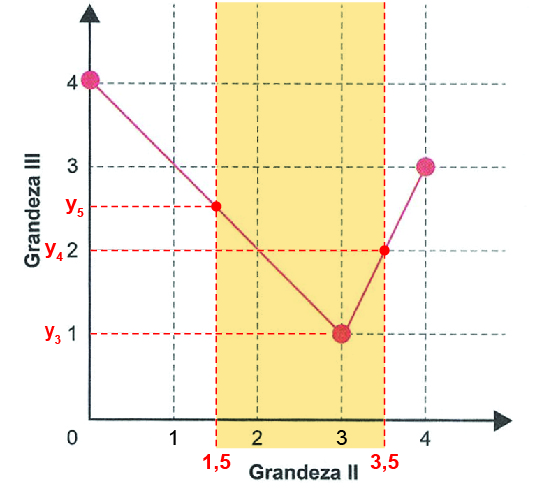 Para o trecho de 0 a 3, a partir dos pontos (0,4) e (3,1), conclui-se que a relação entre as grandezas para o intervalo de 0 a 3 é y = –x + 4, y3 = 1 e, para x = 1,5 , obtemos y5 = 2,5.
Para o trecho de 0 a 3, a partir dos pontos (0,4) e (3,1), conclui-se que a relação entre as grandezas para o intervalo de 0 a 3 é y = –x + 4, y3 = 1 e, para x = 1,5 , obtemos y5 = 2,5.
Para o trecho de 3 a 4, a partir dos pontos (3,1) e (4,3), conclui-se que a relação entre as grandezas II e III para o intervalo de 3 a 4 é y = 2x – 5 e, para x = 3,5 , obtemos y4 = 2.
Logo, para uma variação de 1 a 3 na grandeza I, a variação na grandeza III é de 1 a 2,5 e o valor máximo assumido pela grandeza III é 2,5.