No plano cartesiano, a reta r, de equação y = – x + 12, intersecta a reta s, de equação y = x + 5, no ponto P. A reta r intersecta o eixo x no ponto R, e a reta s intersecta o eixo y no ponto S, como na figura.
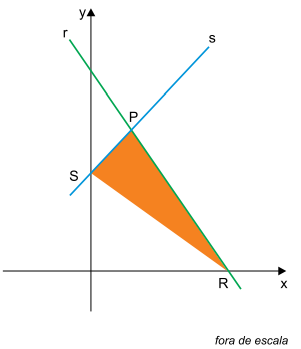
A área do triângulo de vértices PRS é
Inicialmente, vamos determinar as coordenadas do ponto P:
Como , temos
, de modo que as coordenadas do ponto P são (2; 7).
Além disso, vamos determinar a abscissa do ponto de interseção da reta r com o eixo x:
Veja a figura a seguir, que ilustra os resultados obtidos:
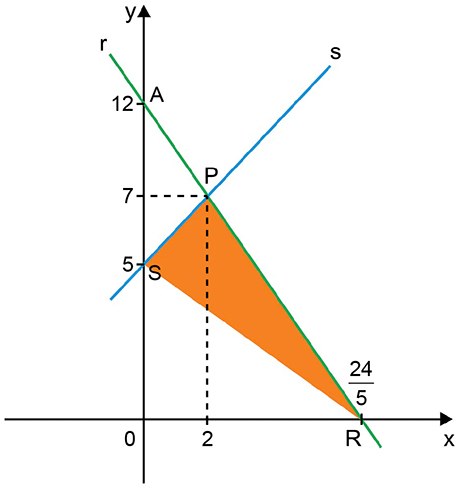
Na figura, foram destacadas as ordenadas das interseções das retas r e s com o eixo y e foram nomeados os pontos A e O respectivamente, o ponto de interseção da reta r com o eixo y e a origem do sistema de coordenadas.
Para calcular a área A do triângulo PRS, podemos subtrair as áreas dos triângulos APS e SRO da área do triângulo ARO:
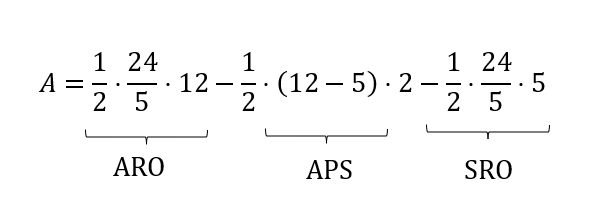
Logo: