O diagrama pressão x volume representa um ciclo termodinâmico efetuado por um gás refrigerante de um sistema de ar condicionado utilizado no processo de resfriamento do interior de um veículo. Nesse processo, o gás absorve calor do interior do veículo (Qint) e libera calor para o meio exterior (Qext).
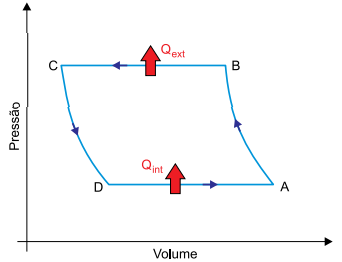
Sabe-se que, nesse ciclo:
• AB representa uma compressão adiabática;
• BC representa uma compressão isobárica;
• CD representa uma expansão adiabática;
• DA representa uma expansão isobárica.
Considerando o gás ideal e a primeira lei da termodinâmica, o gás do sistema de ar condicionado sofreu aquecimento nas transformações
Vamos analisar cada uma das transformações.
I. Transformação AB: compressão adiabática.
Por ser adiabática, o gás não troca calor com o meio exterior. Porém, por haver uma compressão, o gás recebe energia (mecânica) do meio. Nesse caso, trabalho da força aplicada pelo gás é negativo. De acordo com a 1ª lei da Termodinâmica (), como Q = 0 e τ < 0, conclui-se que ΔU > 0. Assim sendo, nessa transformação, o gás foi aquecido.
II. Transformação BC: compressão isobárica.
Para essa transformação, o caminho mais simples é analisar a relação de Clapeyron.
p·V = n·R·T
Uma vez que p, n e R são constantes, podemos reescrever a relação acima da seguinte maneira:
Ou seja:
V = constante · T
Assim, a temperatura absoluta T é diretamente proporcional ao volume. Uma vez que houve uma redução no volume do gás (compressão), pode-se concluir que, nessa transformação, o gás foi submetido a um resfriamento.
III. Transformação CD: expansão adiabática.
Analogamente à análise procedida no item I), por ser adiabática, o gás não troca calor com o meio exterior. Mas, por haver uma expansão, o gás cede energia (mecânica) ao meio. Nesse caso, trabalho da força aplicada pelo gás é positivo. De acordo com a 1ª lei da Termodinâmica (), como Q = 0 e τ > 0, conclui-se que ΔU < 0. Assim sendo, nessa transformação, o gás foi resfriado.
IV. Transformação DA: expansão isobárica.
Analogamente ao caso analisado no item II), para essa transformação, o caminho mais simples é observar a relação de Clapeyron.
p·V = n·R·T
Uma vez que p, n e R são constantes, tem-se:
Ou seja:
V = constante · T
Assim, a temperatura absoluta T é diretamente proporcional ao volume. Uma vez que houve um aumento no volume ocupado pelo gás (expansão), pode-se concluir que, nessa transformação, o gás foi submetido a um aquecimento.
Resumindo, o gás foi submetido a um aquecimento nas transformações AB e DA.