Uma partícula, de peso 8,0 × 10–6 N e eletrizada com carga positiva de 2,0 × 10–8 C, move-se com velocidade horizontal constante de 2,5 × 103 m/s no plano XY e na direção e no sentido positivo do eixo X de um sistema de eixos tri-ortogonais, como mostrado na figura, na qual representa a aceleração gravitacional.
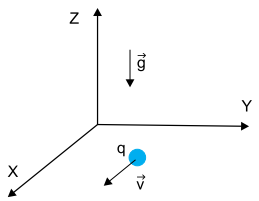
Para que essa condição seja possível, desprezando-se possíveis forças de resistência ao movimento, deve atuar sobre a partícula uma força vertical, com sentido para cima, que compense o peso.
a) Suponha que a partícula seja mantida nessa situação pela ação de um campo elétrico uniforme. Usando como referência o sistema de eixos da figura, determine a direção e o sentido desse campo elétrico e calcule a sua intensidade, em N/C.
b) Suponha que a partícula seja mantida nessa situação pela ação de um campo magnético uniforme. Usando como referência o sistema de eixos da figura, determine a direção e o sentido desse campo magnético e calcule a sua intensidade, em teslas.
a) Como se afirma no próprio enunciado, a força elétrica que equilibra o peso deve ter direção vertical e sentido para cima.
Uma vez que a partícula possui carga elétrica positiva, o campo elétrico apresenta o mesmo sentido da força elétrica.
Assim, o campo elétrico apresenta direção e sentido do eixo Z.
A intensidade da força elétrica é dada por: .
Uma vez que ela deve equilibrar a força peso:
Fe = P
|q|·E = P
Fazendo as substituições numéricas:
2·10-8·E = 8·10-6
Portanto:
E = 400 N/C
b) Analogamente ao item anterior, a força de natureza magnética deve ser vertical e com sentido para cima.
Posicionando a mão direita, conforme a regra número 2, temos:
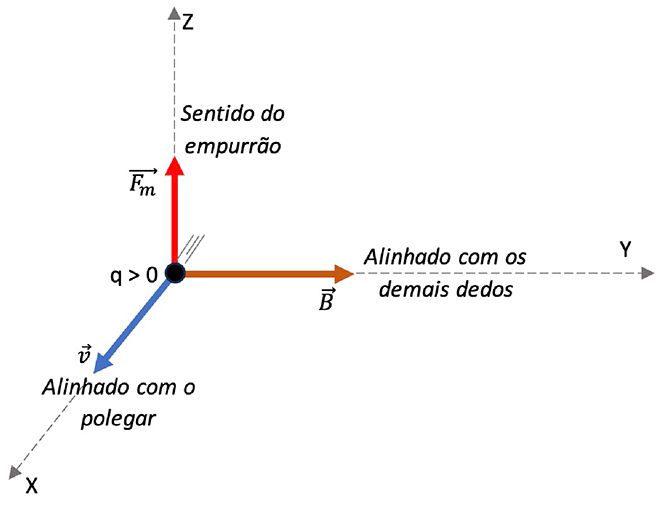
Portanto, conclui-se que o campo magnético, indicado por , deve ter direção e sentido do eixo Y.
A intensidade da força magnética é dada por: Fm = |q|·v·B·sen θ, em que, para esse caso, θ = 90o e sen 90o = 1.
Uma vez que a força magnética deve equilibrar a força peso:
Fm = P
|q|·v·B = P
Fazendo as substituições numéricas:
2·10-8·2,5·103·B = 8·10-6
Portanto:
B = 0,16 T