A figura mostra a trajetória de um raio de luz monocromática que incide perpendicularmente à superfície de um prisma no ponto P. O prisma é constituído do material , no qual a luz se propaga com velocidade de 1,5 × 105 km/s, e está imerso no material
.
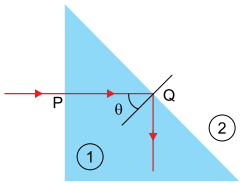
a) Qual fenômeno óptico ocorre com o raio de luz no ponto P? Mostre que a expressão matemática que representa a lei referente a esse fenômeno é válida na situação representada na figura.
b) Sabendo que a luz se propaga no vácuo com velocidade de 3,0 × 105 km/s, calcule o índice de refração absoluto do material . Sabendo que o seno do ângulo θ vale 0,75, calcule o maior valor do índice de refração absoluto do material
para que ocorra o fenômeno mostrado no ponto Q.
a) O fenômeno óptico que ocorre em P é a refração.
A lei da refração é dada por:
sen i·n1 = sen r·n2
Para a refração em P, i = 0. Logo, sen i = 0.
Assim:
0·n1 = sen r ·n2
Uma vez que n1 e n2 não são nulos, conclui-se que sen r = 0. Portanto, r = 0, estando coerente com o indicado no esquema.
b) O índice de refração absoluto do meio 1 é dado por:
Uma vez que, no ponto Q, ocorre o fenômeno da reflexão total, conclui-se que o ângulo de incidência θ é superior ao ângulo limite L desse par de meios.
Algebricamente: θ > L.
Como estamos operando com ângulos do primeiro quadrante trigonométrico, a seguinte conclusão é válida:
Se θ > L ⇒ sen θ > sen L, em que:
e
Sabe-se que o fenômeno da reflexão total só pode ocorrer no interior dos meios mais refringentes. Dessa maneira, o meio 1 é mais refringente que o meio 2. Daí se conclui que:
nmaior = n1 = 2,0
nmenor = n2 = ?
Assim sendo, combinando-se as informações acima:
sen θ > sen L
Substituindo os valores numéricos:
Portanto: n2 < 1,5
Por se tratar de um intervalo aberto, não existe um maior valor do índice de refração do meio 2, conforme perguntado nesse item.
Todavia, pelo questionamento proposto pela banca, é possível inferir que o valor questionado deve ser 1,5.