Um quadrado de área 5 está inscrito em um quadrado de área 9, formando 4 triângulos retângulos congruentes.

a) Determine a área de um desses triângulos retângulos.

b) Determine a razão entre o menor cateto e o maior cateto desses triângulos retângulos.

Considere a figura a seguir, em que o quadrado ABCD tem área 9 e o quadrado EFGH tem área 5.

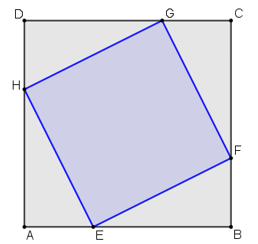
a) Seja A a medida da área de cada triângulo retângulo. Então 5 + 4 A = 9 ⇔ A = 1.

b) Seja L a medida do lado do quadrado ABCD e ℓ a medida do lado do quadrado EFGH. Como os dois quadrados possuem, respectivamente, áreas iguais a 9 e 5, temos que L2 = 9 ⇔ L = 3 e começar estilo tamanho matemático 14px caligráfica l ao quadrado espaço igual a espaço 5 espaço seta dupla para a esquerda e para a direita espaço caligráfica l espaço igual a espaço raiz quadrada de 5 fim do estilo.

Além disso, seja AE = BF = CG = DH = x. Como L = 3, temos AH = BE = CF = DG = 3 - x, com x < 3 - x. Aplicando o Teorema de Pitágoras em um dos triângulos retângulos:

começar estilo tamanho matemático 14px tabela linha com célula com reto x ao quadrado espaço mais espaço parêntese esquerdo 3 espaço menos espaço reto x parêntese direito ao quadrado espaço igual a espaço raiz quadrada de 5 ao quadrado espaço seta dupla para a esquerda e para a direita fim da célula linha com célula com reto x ao quadrado espaço mais espaço 9 espaço menos espaço 6 reto x espaço mais espaço reto x ao quadrado espaço igual a espaço 5 espaço seta dupla para a esquerda e para a direita fim da célula linha com célula com reto x ao quadrado espaço menos espaço 3 reto x espaço mais espaço 2 espaço igual a espaço 0 espaço seta dupla para a esquerda e para a direita fim da célula linha com célula com reto x espaço igual a espaço 1 espaço ou espaço reto x espaço igual a espaço 2 fim da célula fim da tabela fim do estilo

Como x < 3 - x, devemos ter x = 1. Assim, os catetos dos triângulos retângulos medem x = 1 e 3 - x = 2 e a razão entre o menor cateto e o maior cateto é começar estilo tamanho matemático 14px 1 meio fim do estilo.