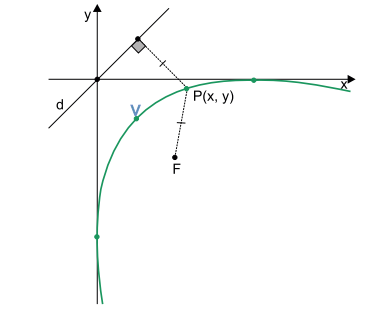
Uma parábola é uma curva formada por todos os pontos P(x, y) do plano que estão igualmente distantes de um ponto fixo F (chamado foco) e de uma reta fixa d (chamada diretriz). A parábola do gráfico a seguir tem por vértice o ponto V, o foco F = (4, –4), e diretriz d: y = x.

a) Sabendo que nessa parábola o vértice V é ponto médio entre o foco F e a origem (0, 0), determine as coordenadas do vértice V da parábola.

b) O módulo da expressão algébrica x – y é denotado por |x – y|, e sabe-se que |x – y|2 = (x – y)2. A distância dP,d entre um ponto P(x, y) do plano e a reta d: y = x é dada por dP,d = começar estilo tamanho matemático 14px numerador abre barra vertical reto x espaço menos espaço reto y fecha barra vertical sobre denominador raiz quadrada de 2 fim da fração. fim do estilo Para determinar a equação de uma parábola, desenvolve-se a equação dP,F = dP,d, em que dP,F é a distância entre o ponto P(x, y) e o foco F da parábola. Com base nessas informações, determine e desenvolva a equação da parábola representada no gráfico.

a) Sendo V o ponto médio entre F(4, –4) e O(0, 0), suas coordenadas são dadas pelo par ordenado começar estilo tamanho matemático 14px abre parênteses numerador 4 espaço mais espaço estreito 0 sobre denominador 2 fim da fração vírgula espaço numerador menos 4 espaço mais 0 sobre denominador 2 fim da fração fecha parênteses fim do estilo. Logo, temos V(2, -2).

Resposta: abscissa 2 e ordenada –2.

b) De começar estilo tamanho matemático 14px reto d com reto P vírgula reto F subscrito fim do subscrito espaço igual a espaço reto d com reto P vírgula reto d subscrito fim do subscrito fim do estilo temos começar estilo tamanho matemático 14px raiz quadrada de parêntese esquerdo reto x espaço menos espaço 4 parêntese direito ao quadrado espaço mais parêntese esquerdo reto y espaço menos espaço 4 parêntese direito ao quadrado espaço fim da raiz espaço igual a espaço numerador abre barra vertical reto x espaço menos espaço reto y fecha barra vertical sobre denominador raiz quadrada de 2 fim da fração fim do estilo. Tomando os quadrados de ambos os membros, segue:

começar estilo tamanho matemático 14px parêntese esquerdo reto x espaço menos espaço 4 parêntese direito ao quadrado espaço mais parêntese esquerdo reto y espaço menos espaço 4 parêntese direito ao quadrado espaço espaço igual a espaço abre parênteses reto x espaço menos espaço reto y fecha parênteses ao quadrado sobre 2 fim do estilo

começar estilo tamanho matemático 14px 2 reto x ao quadrado espaço menos espaço 16 reto x espaço mais espaço 32 espaço mais 2 reto y ao quadrado espaço mais espaço 16 reto y espaço mais espaço estreito 32 espaço igual a espaço reto x ao quadrado espaço menos espaço 2 xy espaço mais espaço reto y ao quadrado fim do estilo

Error converting from MathML to accessible text. começar estilo tamanho matemático 14px abre parênteses reto x espaço mais espaço estreito reto y fecha parênteses ao quadrado espaço menos espaço 16 parêntese esquerdo reto x espaço menos espaço reto y parêntese direito espaço mais espaço 64 espaço igual a espaço 0 fim do estilo

Resposta: começar estilo tamanho matemático 14px abre parênteses reto x espaço mais espaço estreito reto y fecha parênteses ao quadrado espaço menos espaço 16 parêntese esquerdo reto x espaço menos espaço reto y parêntese direito espaço mais espaço 64 espaço igual a espaço 0 fim do estilo