A figura mostra, fora de escala, duas cordas homogêneas, 1 e 2, de densidades lineares de massa µ1 e µ2 = 3µ1, conectadas no ponto P. Nessa figura, observa-se uma onda propagando-se para a direita na corda 1, com velocidade v1 e frequência f1, antes de refratar para a corda 2, onde se propagará com velocidade e frequência v2 e f2, respectivamente.
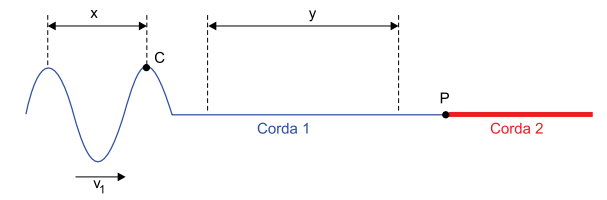
Sabe-se que no mesmo intervalo de tempo Δt = 2 s em que essa onda percorrer o trecho de comprimento y, na corda 1, o ponto C, indicado na figura, realizará quatro oscilações completas na vertical. Sendo x a distância entre duas cristas consecutivas na corda 1 e sabendo que o sistema formado pelas duas cordas é submetido a uma força de tração de intensidade constante,
a) obtenha o valor de f1, em Hz, e calcule o valor da razão
b) obtenha o valor de f2, em Hz, e calcule o valor da razão
a) De acordo com o enunciado, durante o intervalo de tempo de 2 s, o ponto C da corda 1 realiza quatro oscilações completas. Desse modo, é possível determinar a frequência f1, como apresentado a seguir:
Sendo x a distância entre duas cristas consecutivas na corda 1, ela coincide com o comprimento de onda e, portanto, o intervalo de tempo para que ocorra essa propagação é o período da onda (T1):
Desse modo, no intervalo de tempo de 2 s, a onda percorre a distância y, correspondente à quatro vezes o comprimento de onda:
b) Como na refração de uma onda a frequência não se altera, tem-se:
Além disso, para se determinar a relação , pode-se inicialmente utilizar a equação de Taylor:
Como as cordas estão submetidas a mesma tração, pode-se relacionar as velocidades de propagação das ondas: