Para demonstrar as leis da reflexão e da refração luminosa, foi montado o aparato ilustrado na figura, constituído por um aquário de vidro transparente contendo glicerina até certa altura, por dois espelhos planos, E1 e E2, e por uma fonte de laser. O espelho E1 está apoiado na parede lateral esquerda e no fundo do aquário. O espelho E2 está apoiado no fundo horizontal do aquário, com sua face refletora voltada para cima.
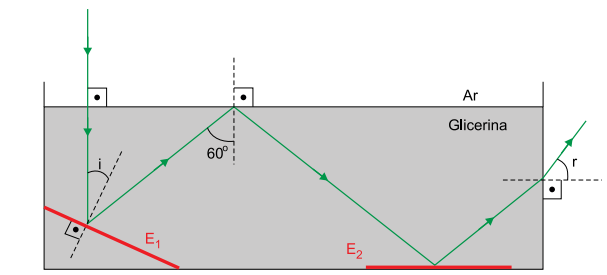
Um feixe de laser propagando-se pelo ar incide perpendicularmente na superfície da glicerina e, após a refração, sofre uma reflexão no espelho E1, uma reflexão total na interface glicerina–ar, nova reflexão no espelho E2 e refrata para o ar na face lateral direita do aquário. Adote 1,0 e 1,5 para os índices de refração absolutos do ar e da glicerina, respectivamente, e c = 3,0 ∙ 108 m/s.
a) Calcule, em m/s, a velocidade de propagação do laser na glicerina e, considerando as informações da figura, obtenha, em graus, o ângulo de incidência (i) desse feixe no espelho E1.
b) Obtenha o seno do ângulo limite para refração na interface glicerina–ar e o seno do ângulo de refração (r) quando o feixe de laser emerge para o ar, na face lateral direita do aquário.
a) De acordo com a definição do índice de refração, é possível determinar a velocidade de propagação do laser na glicerina, como apresentado a seguir:
Além disso, é possível determinar o ângulo de incidência (i) do laser no espelho E1, considerando a figura a seguir e que, no fenômeno da reflexão, o ângulo de incidência (i) é igual ao ângulo de reflexão (r):
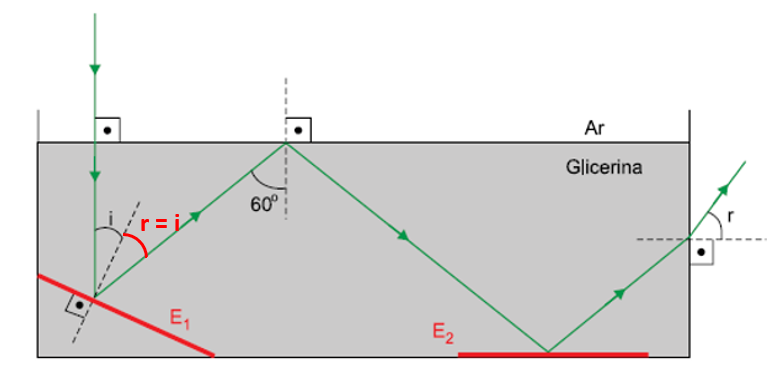
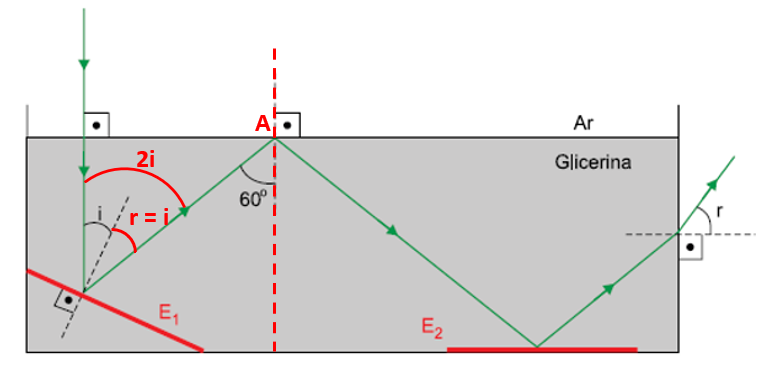
Da figura acima, pode-se notar que o raio incidente (e o refratado) são perpendiculares à superfície de separação e, portanto, possuem direção paralela à direção da reta normal à superfície de separação no ponto A. Desse modo, tem-se que 2.i é igual a 60º, como ilustrado a seguir:
b) Para se determinar o seno do ângulo limite (L), pode-se utilizar a expressão a seguir:
Além disso, para se determinar o seno do ângulo de refração (r), pode-se considerar a figura a seguir considerando que, na reflexão total, os ângulos de incidência e de reflexão são iguais:
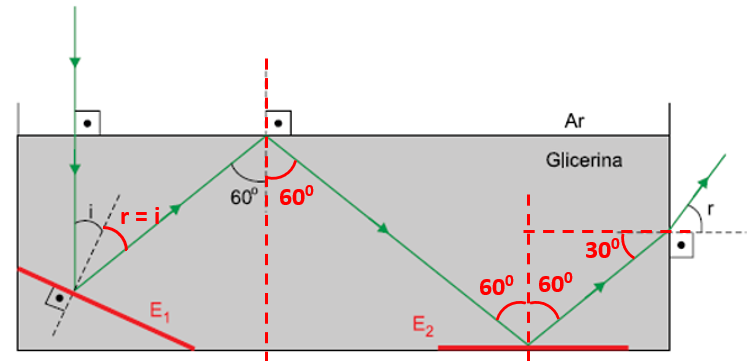
Do esquema acima, é possível utilizar a lei de Snell na superfície de separação de separação vertical entre a glicerina e o ar (à direita da figura):