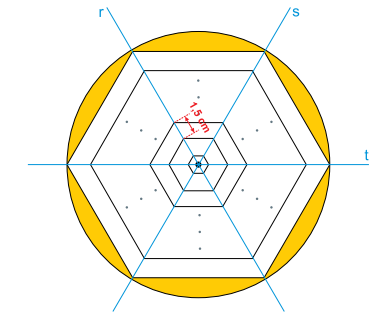
A figura representa uma sequência de n hexágonos regulares concêntricos, cortados pelas retas r, s e t. O menor dos hexágonos tem lado de 1 cm e a distância entre vértices vizinhos de dois hexágonos consecutivos é sempre igual a 1,5 cm.
a) Calcule a medida do lado do 20º hexágono da figura. Sendo Ln a medida, em centímetros, do lado no n-ésimo hexágono da figura, determine a fórmula de Ln em função de n > 1.
b) Sabendo que a região destacada em amarelo na figura é determinada pelo círculo que circunscreve o n-ésimo hexágono da figura e esse hexágono, determine An, que denota a fórmula para o cálculo da área dessa região, em cm2, em função de n > 1.
a) As medidas dos lados dos hexágonos formam uma progressão aritmética de primeiro termo e razão
, logo:
b) A área An é dada pela área do círculo de raio Ln, menos a área do hexágono de lado Ln, ou seja: