A figura representa três ruas paralelas na vertical, cruzadas por quatro ruas paralelas na horizontal. Os veículos só podem percorrer essas ruas, e no sentido das setas.
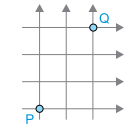
Um taxista decide ir de P para Q por uma das duas regras a seguir:
I. menor caminho que liga os pontos P e Q;
II. menor caminho que liga os pontos P e Q sem que percorra três quarteirões contíguos na mesma rua. Por exemplo, a situação a seguir não é permitida:
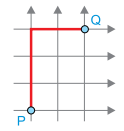
a) Calcule o total de caminhos possíveis pela regra I e o total de caminhos possíveis pela regra II.
b) Considere agora cinco ruas paralelas na vertical, cruzadas por seis ruas paralelas na horizontal, com o sentido de trânsito das ruas indicado pelas setas, conforme representado pela figura.
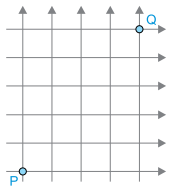
Calcule o total de caminhos possíveis para ir de P até Q pelo menor caminho em que haja, no percurso total, uma sequência de 4 quarteirões contíguos em uma mesma rua na vertical, mas não 5.
a) Denotando por D cada vez que o taxista avança uma unidade de quarteirão à direita e C cada vez que ele avança uma unidade de quarteirão acima, todo menor caminho que liga P a Q pode ser representado por uma sequência da forma (C,C,C,D,D). Assim, o total de caminhos na condição I é dado por todas as permutações dessa sequência, ou seja, .
Destes 10 caminhos, existem somente 3 deles em que o taxista percorre três quarteirões contíguos na mesma rua (percorrendo todos os quarteirões de uma mesma rua vertical). Desta forma, o total de caminhos na condição II é dado por 10 – 3 = 7.
b) Primeiramente note que qualquer caminho nas condições do enunciado é uma permutação da sequência (D,D,D,D,C,C,C,C,C), com a condição de que deve haver exatamente quatro C´s juntos.
Com isso, podemos dividir o problema em dois casos:
O trecho C,C,C,C aparece no início ou no final da sequência, seguido (ou precedido) de uma letra D (como CCCCD ou DCCCC). Nesse caso, falta permutar as letras restantes – C , D , D , D – de modo que o total de sequências nessas condições é dado por ;
O trecho C,C,C,C não aparece no início ou no final da sequência; neste caso, ele deve vir precedido e seguido de uma letra D (formando DCCCCD). Com isso, permuta-se o ‘bloco’ DCCCCD e as demais letras da sequência – C , D , D – de modo que o total de sequências nessas condições é dado por .
Portanto, o total de caminhos possíveis é 8 + 12 = 20.