Uma prova de estatística, valendo de 0 a 10 pontos, foi realizada por 253 alunos, sendo que nenhum tirou nota menor ou igual a 6. O histograma da figura 1 indica a distribuição das notas. Ainda que o eixo com a frequência de alunos em cada faixa de notas tenha sido omitido, foi fornecida a área de cada barra do histograma. A figura 2 ilustra o cálculo da mediana das notas.
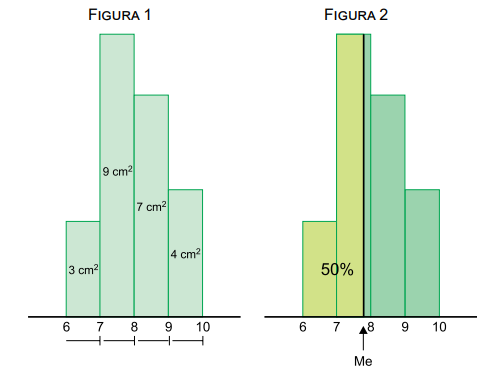
a) Calcule a porcentagem aproximada de alunos que tiraram nota menor ou igual a 7. Calcule a quantidade de alunos que tiraram nota maior que 8.
b) Calcule a média (M) e a mediana (Me) das notas usando aproximação de duas casas decimais, quando necessário.
a) Os alunos que tiraram nota menor ou igual a 7 possuem notas no intervalo ]6,7]. Do gráfico, tem-se que a porcentagem pedida é dada por . Além disso, como os alunos que tiraram nota maior que 8 possuem notas no intervalo ]8,10], então a quantidade pedida é dada por
.
b) A média M é tal que
Já a mediana Me, observa-se que ela é o valor da abscissa cuja reta vertical está indicada na Figura 2. Como a área total da região vale 3 + 9 + 7 + 4 = 23 cm2, então 50% desta área vale 11,5 cm2 e, assim, observe a figura a seguir:
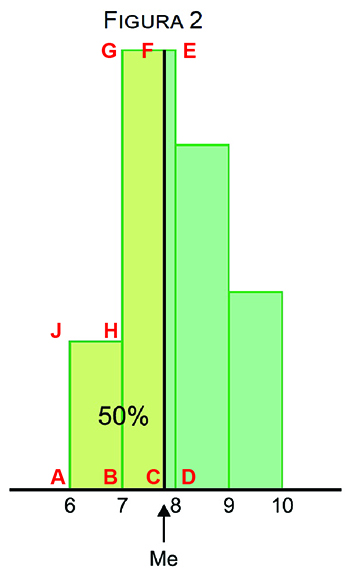
Como a área do retângulo ABHJ vale 3 cm2 e a área do polígono ACFGHJ vale 11,5 cm2, então a área do retângulo BCFG vale 8,5 cm2. Além disso, dado que os retângulos BCFG e BDEG possuem a mesma altura, então pode-se escrever:
Portanto, a mediana Me vale, aproximadamente, 7 + 0,94 = 7,94.