A velocidade do som no ar, em m/s, pode ser calculada, com boa aproximação, pela expressão v = 330 + 0,6 · θ, em que θ é a temperatura do ar, expressa em ºC.
a) Calcule a frequência, em Hz, de uma onda sonora de comprimento de onda 0,57 m que se propaga no ar a 20 ºC.
b) Considere uma onda estacionária produzida dentro de um tubo de 0,70 m de comprimento, aberto em uma de suas extremidades e fechado na outra, conforme a figura.
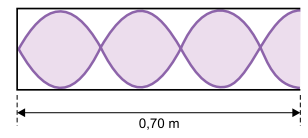
Calcule a temperatura do ar, em ºC, no interior desse tubo para que a frequência do som emitido por ele, na situação mostrada na figura, seja de 945 Hz.
a) Substituindo a temperatura θ = 20 oC na equação fornecida, segue:
Portanto: v = 342 m/s.
Uma vez que o comprimento de onda (λ) vale 0,57 m, na equação fundamental da ondulatória (v = λ·f), podemos determinar a frequência da onda.
342 = 0,57·f
Portanto, f = 600 Hz
b) Pela imagem fornecida, podemos obter o comprimento de onda da onda geradora da onda estacionária no tubo.
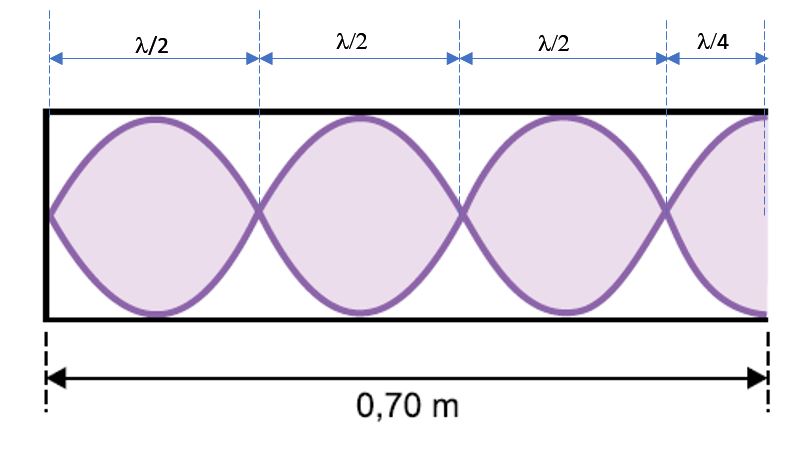
Uma vez que f = 945 Hz, na equação fundamental da ondulatória, temos:
Substituindo esse valor de velocidade na equação fornecida:
Conclui-se que θ = 80 oC.