Um mergulhador e seu equipamento, que totalizam 90 kg, estão em repouso 30 m abaixo da superfície de um lago de águas paradas, sem tocar o fundo do lago, a uma temperatura de 7 ºC.
Considere a densidade da água do lago igual a 103 kg/m3, a aceleração da gravidade igual a 10 m/s2, a pressão atmosférica igual a 105 N/m2 e o ar um gás ideal.
a) Represente, na imagem inserida no campo de Resolução e Resposta, as forças que atuam no mergulhador em repouso na posição mostrada na figura. Calcule a intensidade do empuxo, em N, exercido pela água do lago no mergulhador, nessa posição.
b) Em determinado momento, esse mergulhador libera uma bolha de ar de volume 14 cm3 que sobe à superfície, onde a temperatura é de 27 ºC. Suponha que, em seu movimento de subida, a bolha não se rompa e mantenha-se sempre em equilíbrio térmico com a água do lago. Calcule o volume, em cm3, dessa bolha de ar no momento em que atinge a superfície do lago.
a) As únicas forças aplicadas no mergulhador em repouso são o empuxo, aplicado pela água, e o peso, aplicado pela Terra.
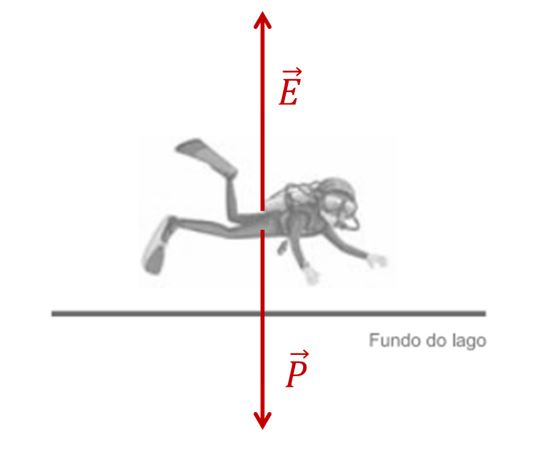
Como o mergulhador está em repouso, a resultante das forças nele aplicadas é nula. Logo, o empuxo e o peso se equilibram:
Sendo m = 90 kg e g = 10 m/s2:
Logo, a intensidade do empuxo é 900 N.
b) A pressão do ar aprisionado na bolha, cujo volume é Vi = 14 cm3, quando ela está no fundo do lago é a soma da pressão atmosférica, ou seja, 1 atm, com aquela exercida por uma coluna de 30 metros de água, ou seja, 3 atm.
Logo, pi = 4 atm. Nessa situação, a temperatura do ar aprisionado pela bolha é 7 oC, ou seja, Ti = 280 K.
A pressão do ar aprisionado na bolha, cujo volume é Vf, quando ela está na superfície corresponde apenas à pressão atmosférica, ou seja, 1 atm. Logo, pf = 1 atm. Nessa situação, a temperatura do ar aprisionado pela bolha é 27o C, ou seja, Tf = 300 K.
Dessa maneira, considerando que o ar aprisionado na bolha seja um gás ideal e que o número de moléculas de ar permaneça constante, podemos escrever:
Logo, o volume da bolha será de 60 cm3.