Em determinado trecho de uma montanha-russa, um carrinho de 300 kg passou por um ponto A com velocidade vA = 1 m/s e por um ponto B com velocidade vB = 5 m/s. Nesse trecho, a linha reta que liga o ponto A ao ponto B é inclinada de um ângulo θ com a direção horizontal, conforme a figura.
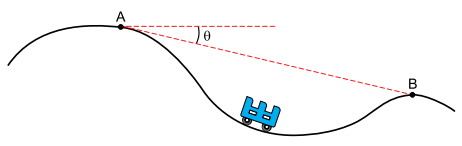
Desprezando as dimensões do carrinho, o atrito e a resistência do ar, adotando g = 10 m/s2, sabendo que sen θ = 0,12 e que o carrinho demorou 4 s para ir do ponto A ao ponto B:
a) Calcule a intensidade da aceleração escalar média, em m/s2, do carrinho no trajeto entre o ponto A e o ponto B. Calcule o trabalho, em J, realizado pela resultante das forças que atuaram sobre o carrinho nesse mesmo trecho.
b) Calcule a distância em linha reta, em metros, do ponto A ao ponto B.
a) A intensidade da aceleração escalar média do carrinho entre os pontos A e B pode ser determinada diretamente pela definição, como segue:
Substituindo-se os dados numéricos fornecidos:
Logo, a aceleração escalar média é de 1 m/s2.
· O trabalho realizado pela resultante entre os pontos A e B pode ser obtido pelo teorema da energia cinética, como segue:
Substituindo-se os dados numéricos fornecidos:
Logo, o trabalho da resultante é 3600 J.
b) Como o atrito e a resistência do ar podem ser desprezadas, as únicas forças aplicadas no carrinho entre os pontos A e B são a força peso e normal de contato
. Logo, a resultante é soma vetorial dessas duas forças:
Dessa maneira:
Como a normal de contato é perpendicular ao deslocamento, seu trabalho é nulo. Portanto:
Utilizando o teorema da energia potencial:
Considerando hB = 0, temos, substituindo-se os dados numéricos fornecidos e obtidos:
Logo, a distância d, em linha reta, entre os pontos A e B pode ser obtida por trigonometria, como segue:
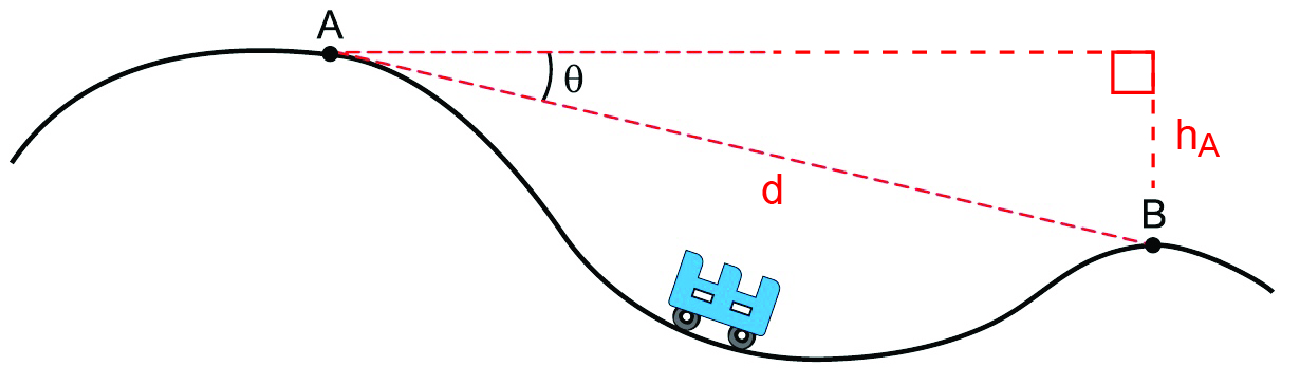
E assim, substituindo-se os dados numéricos fornecidos e obtidos:
Logo, a distância entre os pontos A e B é 10 m.