Um período da vida do físico J. Robert Oppenheimer pouco retratado no recente filme Oppenheimer é o seu Doutorado na Alemanha sob a orientação de Max Born. Em 1927, eles publicaram um trabalho muito importante, que se tornaria uma das bases da física atômica e molecular. A chamada Aproximação de Born-Oppenheimer usa o fato de que a massa dos núcleos é muito maior que a massa dos elétrons para justificar um tratamento independente do movimento dos núcleos e o dos elétrons em átomos e moléculas.

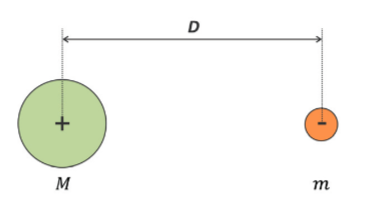
Para ilustrar a validade da aproximação, considere um modelo clássico para o átomo de hidrogênio composto de um próton de massa M e carga +e e um elétron de massa m e carga – e separados por uma distância D, como mostra a figura.

a) Considerando o sistema inicialmente estático, desenhe, na folha de respostas, os vetores das forças elétricas que atuam sobre as duas partículas

Considere agora que as velocidades das cargas estão sempre em sentidos opostos e perpendiculares à linha que une os seus centros, como mostra a figura. Considere também que a única força que atua sobre as partículas é a força elétrica entre elas, de modo que a quantidade de movimento total (ou momento linear total) do sistema é nula. Considere ainda que ambas as cargas estejam em movimento circular uniforme em torno do centro de massa do sistema, de modo que distância entre as duas partículas não se altere.

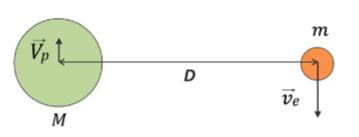
b) Sendo M/m = 1800, calcule a razão entre os intervalos de tempo que o elétron e o pósitron, respectivamente, levam para percorrer um arco de circunferência de mesmo comprimento Δs.

c) Na aproximação de Born-Oppenheimer, pode ser feita a hipótese de que o próton permanece em repouso enquanto o elétron gira em torno dele. Utilizando essa hipótese e supondo ainda que a trajetória do elétron seja uma circunferência de raio D, calcule a energia cinética do elétron em termos de e, de D e da constante eletrostática da Lei de Coulomb k₀.