Considere uma mesma corda de violoncelo vibrando, em situações distintas, conforme os padrões de ondas estacionárias mostrados nos diagramas a seguir, em que a amplitude das vibrações, por clareza, está grandemente ampliada. No diagrama 1, a corda vibra no comprimento L mostrado na figura. No diagrama 2, a corda está pinçada a 2/3 do comprimento L, de modo que não há vibração no terço restante.
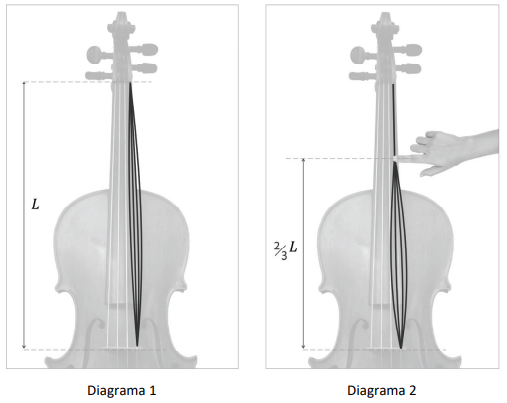
a) Um aluno afirma que, por se tratar de padrões estacionários, a velocidade de propagação de uma onda qualquer na corda é nula. Essa afirmação é correta? Justifique a sua resposta.
b) Considere agora a situação mostrada no diagrama 1. Se o comprimento L fosse de 60 cm, qual seria o comprimento de onda da vibração mostrada nesse diagrama?
c) Suponha agora que a frequência da vibração da corda no padrão mostrado no diagrama 1 seja de 220 Hz. Determine a frequência de vibração da corda no padrão mostrado no diagrama 2.
a) Entre diversas propriedades relacionadas às ondas, uma delas é a sua propagação com transferência de energia sem que haja transferência de matéria. Por esse motivo, a afirmação pode ser considerada incorreta dado que a denominação “ondas estacionárias” não está relacionada a ondas que não se desloquem ou que permaneçam “estáticas”, mas sim ao efeito estacionário dos processos de interferência entre as ondas idênticas que se propagam em sentidos opostos.
b) De acordo com o diagrama 1, pode-se identificar o padrão de formação do 1º harmônico na corda. Sendo assim:
c) De acordo com o diagrama 2, também é possível identificar o padrão de formação do 1º harmônico na corda nesse caso. Sendo assim:
Por se tratar da mesma corda, a velocidade de propagação se mantém constante nas duas situações propostas. Desse modo, tem-se:
V1 = V2
λ1 · f1 = 2 · f2
1,2 · 220 = 0,8 · f2
∴ f2 = 330 Hz