A figura a seguir esboça, no plano cartesiano, a região hachurada delimitada pelo eixo 0x, pelo eixo 0y e pela reta x + y = 4.
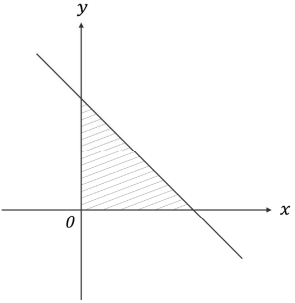
a) Calcule a área da região determinada pela intersecção do plano 0xy com o sólido de revolução gerado pela rotação da região hachurada quando gira em torno do eixo 0y.
b) Calcule o volume do sólido de revolução gerado pela rotação da região hachurada quando gira em torno da reta vertical x = 4.
c) Calcule o volume do sólido de revolução gerado pela rotação da região hachurada quando gira em torno da reta x+ y = 4.
a) Ao rotacionarmos a região hachurada em torno de eixo 0y, obtemos o cone da figura a seguir e a área hachurada é a intersecção com o plano 0xy
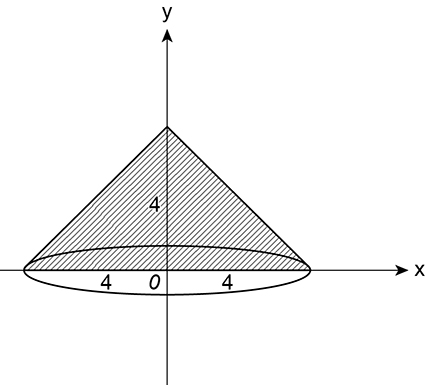
Essa área é dada por
Resposta: 16
b) Ao rotacionarmos a região hachurada em torno da reta vertical x = 4, obtemos o sólido representado a seguir, que é composto por um cilindro com uma cavidade cônica.
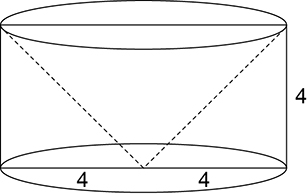
Seu volume V é dado pelo volume do cilindro menos o volume do cone, ou seja:
Resposta:
c) Ao rotacionarmos a região hachurada em torno da reta x + y = 4, obtemos o sólido a seguir, que é composto por dois cones justapostos pela base.
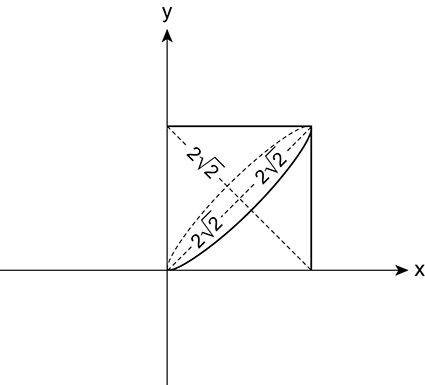
Seu volume V é dado por duas vezes o volume do cone, ou seja:
Resposta: