Vamos admitir que uma corda presa nas extremidades de duas hastes paralelas e de mesma altura descreve uma curva que é dada pela equação y = 2x + 2-x. Uma representação gráfica dessa equação, limitada por duas retas verticais paralelas ao eixo 0y e onde o eixo 0x indica o solo, é dada pela figura. A unidade de medida é o metro (m).
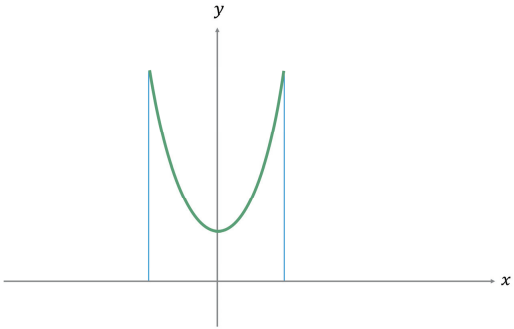
a) Qual a altura mais baixa que a corda assume?
b) Qual será a altura das hastes se a distância entre elas for de 3 m?
c) Qual a distância entre dois pontos da corda que estão a uma altura de 4 m do solo?
a) A altura mais baixa que a corda assume é para x = 0, ou seja y = 20 + 20, y = 2.
Resposta: 2 m.
b) Quando a distância entre as duas hastes for de 3 m, a abscissa da haste à direita é , a sua altura é dada por:
Resposta:
c) Para y = 4, tem-se:
Fazendo 2x = t, vem:
logo, e
Ou
logo, e
A distância entre os dois pontos é:
Resposta: