Considere a parábola P dada pela equação y = x2 e a reta r dada pela equação ax + by + c = 0, onde a, b, e c são constantes reais. Denote por 0 = (0,0) a origem do sistema de coordenadas cartesiano 0xy.
a) Se a = 2, b = −1 e c = 3, determine todos os pontos do plano cartesiano que pertencem, simultaneamente, à reta r e à parábola P.
b) Se a = 4, b = 3 e c = −7, determine o ponto da reta r que está mais próximo de 0.
c) Considere três pontos A, B e C na parábola P, tais que A = (−1,1), B pertence ao primeiro quadrante e os segmentos AB e OC são paralelos. Determine B e C de forma que a distância de B até C seja .
a) Com ,
e
, a reta r é dada pela equação
, ou seja,
Os pontos de intersecção da reta r e da parábola são dados pelo sistema
Resulta, assim, a equação , ou
, cujas raízes são 3 e –1.
Do sistema (S) e x = 3, temos y = 9.
Do sistema (S) e x = –1, temos y = 1.
Resposta: (3, 9) e (–1, 1)
b) Com ,
e
, a reta r é dada pela equação
e o coeficiente angular dela é
Consideremos, agora a reta t, que passa pela origem e é perpendicular à reta r.
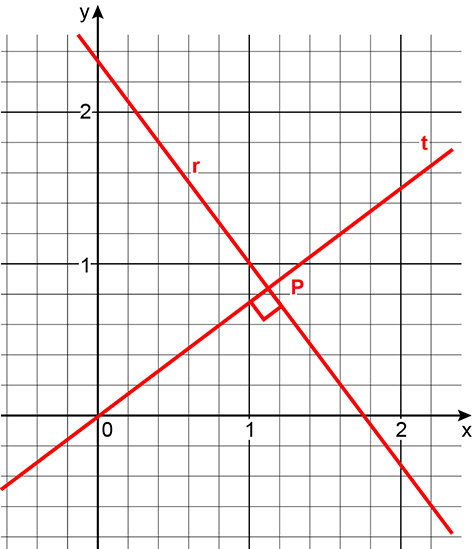
O ponto P dado pela intersecção de r e t é o ponto de r mais próximo de O(0, 0)
O coeficiente angular da reta t é e ela é dada pela equação
O ponto P é dado pelo sistema
Resolvendo esse sistema, obtemos o par ordenado
Resposta:
c) Considere a figura a seguir:
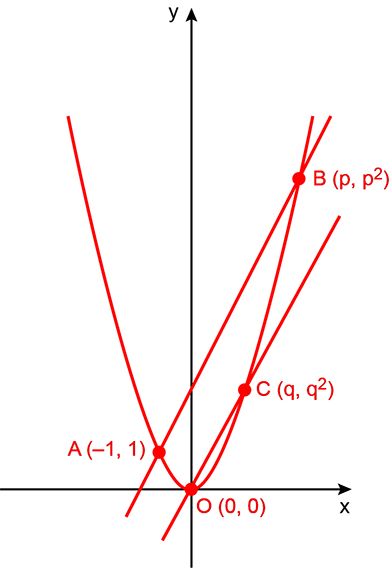
O coeficiente angular da reta é dado por
O coeficiente da reta é dado por
Como essas retas são paralelas, temos p – 1 = q, ou seja, p = q + 1
De , temos
e:
e
ou
(não convém, pois q > 0)
e
Resposta: e