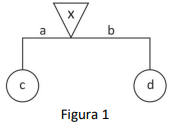
Um móbile matemático é uma figura que simula móbiles físicos. Ela é formada por segmentos de reta e figuras planas com valores numéricos racionais positivos, de forma a buscar um equilíbrio. A figura 1 ilustra um móbile básico matemático. Para ele estar em equilíbrio, os valores devem cumprir as equações x = ac + bd e ac = bd. Quando não aparecem valores para as letras a e b, significa que ambas valem 1.
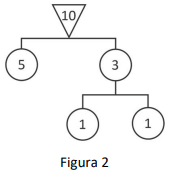
Um móbile pode ser composto por diversos móbiles básicos, como a figura 2. Note que, nele, tem-se 5 = 3 + 1 + 1, mantendo o móbile em equilíbrio.
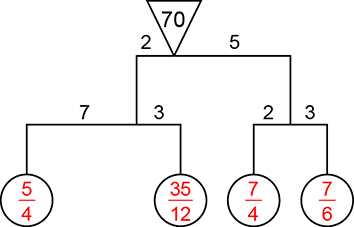
Considerando os móbiles I, II e III, apresentados na folha de respostas, responda ao que se pede:
a) Complete o móbile I, preenchendo as formas geométricas vazias com os valores que faltam para que ele esteja em equilíbrio.
b) Determine n ∈ N para que o móbile II esteja em equilíbrio.
c) Complete o móbile III, preenchendo as formas geométricas vazias com os valores que faltam para que ele esteja em equilíbrio.
O enunciado ilustra um móbile básico como sendo composto por apenas um triângulo e dois círculos. Dessa forma, não é imediato entender como a Figura 2 é composta por mais de um móbile básico, já que apresenta apenas um triângulo.
Para poder resolver a questão, é necessário inferir, a partir do exemplo da Figura 2 e da comparação com a situação física, algumas outras regras.
Para entender o exemplo da Figura 2, considere o seguinte móbile básico inicial:
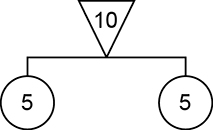
Se adicionássemos outro móbile básico abaixo do círculo da direita, o equilíbrio do móbile inicial seria perturbado, já que o “peso” sustentado pelo braço direito do móbile inicial seria maior que 5. Dessa forma, para se pendurar outro móbile, é necessário que uma parte do “peso” 5 seja utilizada para os círculos do novo móbile.
Assim, podemos entender a bifurcação abaixo do círculo de “peso” 3 na Figura 2 da seguinte forma:
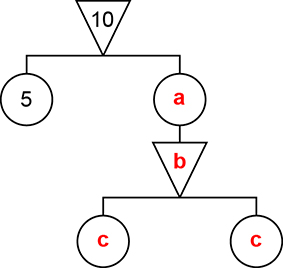
Para que o equilíbrio seja mantido, devemos ter e
. Na Figura 2, foi escolhido o valor
, de modo que devemos ter
e, portanto,
.
Apesar de essa, interpretação não ficar clara de maneira textual no enunciado, ela tem significado físico (a ideia de manter o equilíbrio do móbile).
Feitas as observações, vamos prosseguir com a resolução da questão.
a) Veja a figura a seguir, modificada de acordo com as observações feitas anteriormente.
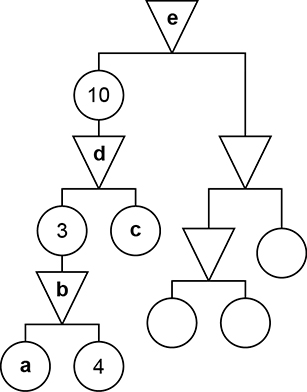
Começando pelo móbile básico mais inferior à esquerda, temos:
Agora, vamos preencher os “pesos” das demais formas geométricas. Considerando que os dois círculos mais inferiores à direita devem ter o mesmo “peso” para manter o equilíbrio, podemos preencher a figura:
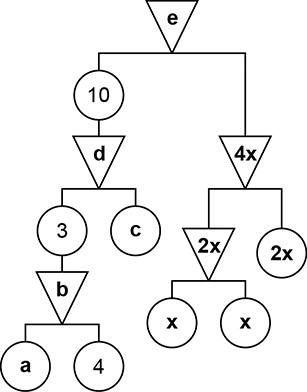
Assim, devemos ter , ou seja,
e, portanto,
. Voltando à forma como a figura foi apresentada na folha de respostas, chegamos a:
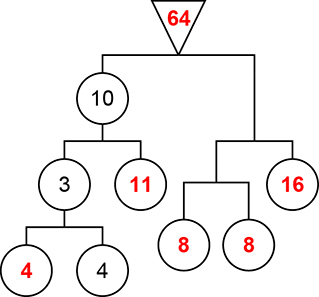
b) Veja a figura a seguir, em que os “pesos” foram representados pelas letras e
:
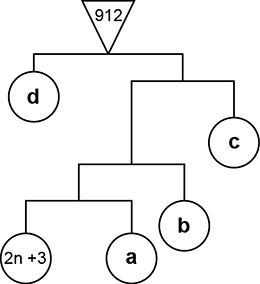
Pelas observações feitas anteriormente, devemos ter:
Dessa forma:
c) Veja a figura a seguir, modificada de acordo com as observações feitas anteriormente.
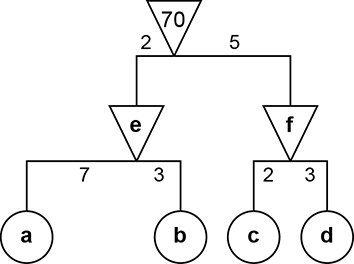
Considerando o móbile superior, temos:
Resolvendo esse sistema, obtemos e
.
Considerando o móbile mais inferior à esquerda:
Como , podemos resolver o sistema anterior, obtendo
e
.
Por fim, considerando o móbile mais inferior à direita:
Como , resolvendo o sistema, obtemos
e
.
Voltando à forma como a figura foi apresentada na folha de respostas, chegamos a: