Na figura abaixo, ABCD representa um terreno quadrado cujos lados medem 10m, coberto por grama alta. O ponto E é o ponto médio do lado AD; o segmento EF, paralelo ao lado DC, representa um muro de 5m de comprimento e bem alto, sendo, portanto, intransponível.
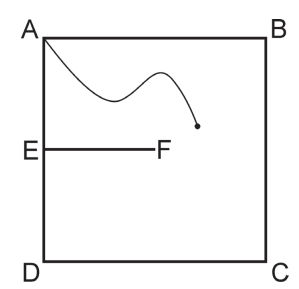
Um cortador de grama robótico será usado para cortar a grama do terreno. Ele será ligado na energia no ponto A e seu cabo de energia tem comprimento de 10m. Para funcionar, ele tem que estar ligado todo o tempo na tomada.
a) Ao usar o aparelho para cortar a grama do terreno, uma pessoa tenta se aproximar, ao máximo, do lado CD. Nessa situação, calcule a distância que falta para o cortador de grama alcançar o lado CD. Justifique.
b) O robô não conseguirá cortar a grama do terreno todo, já que seu fio é curto e o muro é um obstáculo. Qual a maior área do terreno que o robô conseguirá cortar a grama?
a) Supondo que a pessoa e o robô ocupem o mesmo ponto, a figura a seguir representa a situação descrita, sendo G o ponto ocupado pelo robô e H o ponto médio do lado . Dessa forma, GH é a distância pedida.
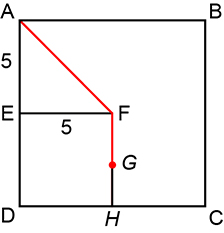
Como o triângulo AEF é retângulo, temos:
O comprimento do fio, de 10 m, é a soma das medidas AF e AG, ou seja:
Por fim, como FH = 5, devemos ter:
A distância pedida é, portanto, de .
b) Primeiramente, note que, como , todos os pontos do triângulo AEF podem ser atingidos pelo robô.
Em seguida, imagine que o robô esteja com o fio totalmente esticado, ocupando o ponto B. A partir dessa posição, mantendo o fio completamente esticado, é possível cortar a grama de todos os pontos de um setor circular com centro em A e raio medindo 10 m, enquanto o fio não encostar no ponto F. A figura a seguir ilustra essa afirmação, sendo G o ponto ocupado pelo robô na iminência do fio tocar o ponto F.
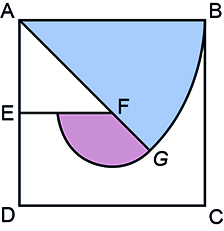
A partir daí, mantendo o fio completamente esticado, é possível varrer a área de um setor circular com centro em F e raio medindo (determinado no item anterior), até que o robô ocupe um ponto do lado
. A figura a seguir mostra toda a área cuja grama pode ser cortada, assim como os ângulos centrais dos setores circulares.
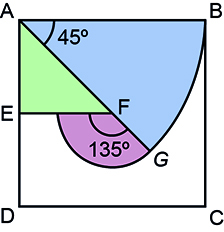
A área do triângulo AEF vale:
O setor circular maior tem área igual a:
O setor circular menor, por sua vez, tem área igual a:
Dessa forma, a maior área cuja grama o robô consegue cortar vale