A figura abaixo mostra uma pirâmide e um cubo, que compartilham uma aresta da base da pirâmide. A pirâmide tem altura medindo 1m; sua base, bem como os lados do cubo, são quadrados de lados medindo 1m.
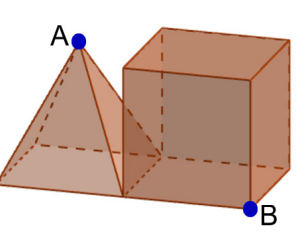
a) Um sólido é formado pela união desses dois objetos. Qual é o seu volume?
b) Determine a distância do ponto A (vértice superior da pirâmide) até o ponto B (vértice “frontal” da base do cubo que não está na aresta em comum com a pirâmide).
a) O volume do sólido é dado pela soma dos volumes da pirâmide e do cubo. A pirâmide tem área da base igual a 12 = 1 m2 e altura 1 m, de modo que seu volume é , e o cubo tem aresta medindo 1 m, de modo que seu volume é 13 = 1 m3.
Assim, o volume do sólido formado é igual a .
b) O enunciado não descreve a pirâmide como regular, ou seja, não necessariamente o vértice A tem projeção ortogonal sobre o centro de sua base. Porém, se esse não for o fato, faltam informações para responder à pergunta proposta.
Dessa forma, admitindo que a pirâmide é regular, veja a figura a seguir, que exibe os segmentos e
, sendo C o centro da base da pirâmide e, portanto, a projeção ortogonal do vértice A sobre essa base.
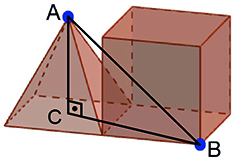
O segmento tem medida igual à altura da pirâmide, ou seja, 1 m. Para determinar a medida do segmento
, veja a figura a seguir, que exibe as bases da pirâmide e do cubo e o ponto D, de modo que
é o apótema da base da pirâmide e, portanto, D é ponto médio de uma das arestas da base.
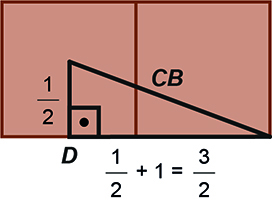
Pelo teorema de Pitágoras, temos:
Na figura do enunciado, como o triângulo ACB é retângulo, temos:
O segmento mede
ou
.
Observação: o enunciado poderia ter sido escrito de forma mais clara e precisa. Além da falha já mencionada, é impreciso se referir às faces laterais de um cubo como “lados” do cubo.