Uma escola tem 4 turmas: A, B, C e D. As turmas B e C têm, cada uma delas, uma quantidade x de alunos, e as turmas A e D têm, cada uma delas, uma quantidade 3x de alunos.
Em determinado momento do ano, foi realizada uma eleição para o Grêmio Estudantil, e havia duas candidaturas: a da Chapa 1 e a da Chapa 2. O gráfico abaixo mostra o resultado da votação, em percentual, em cada uma das turmas. Sabe-se que todos os alunos da escola votaram, e não houve nenhum voto branco ou nulo.
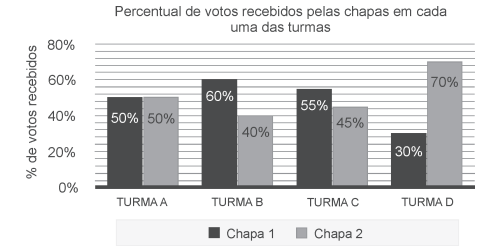
Há duas propostas sobre como definir a chapa vencedora da eleição:
• Proposta 1: vence a eleição a chapa que receber a maior quantidade de votos, considerando o total de votos da escola.
• Proposta 2: vence a eleição a chapa que ficar em primeiro lugar (isto é, a que receber mais votos) no maior número de salas.
a) Qual chapa seria a vencedora se fosse adotada a Proposta 1? Haverá alguma mudança se a Proposta 2 for adotada? Justifique suas respostas.
b) Sabendo que a escola tem 160 alunos, informe, na tabela disposta no campo de resolução, quantos alunos cada uma das turmas tem, e justifique sua resposta.
a) Inicialmente, vamos contabilizar as quantidades de votos por chapa, por turma:

Dessa forma, a chapa 1 recebeu um total de 1,5x + 0,6x + 0,55x + 0,9x = 3,55x votos e, a chapa 2, um total de 1,5x + 0,4x + 0,45x + 2,1x = 4,45x votos. Portanto, de acordo com a Proposta 1, a chapa 2 é a vencedora.
Considerando a proposta 2, então as duas chapas empatam na turma A, a chapa 1 fica em primeiro lugar nas turmas B e C e a chapa 2 vence na turma D, apenas. Ou seja, de acordo com a Proposta 2, a chapa 1 seria a vencedora.
b) Como as turmas A e D têm 3x alunos e, as turmas B e C, x alunos, o total de alunos da escola é 3x + x + x + 3x = 8x. Do enunciado, tem-se que esse total é de 160 alunos, ou seja:
Dessa forma, as turmas A e D têm 60 alunos e, as turmas B e C, 20 alunos. Preenchendo a tabela, tem-se:
