Um par de câmeras idênticas foi posicionado para realizar “visão estereoscópica”, que é um procedimento que usa as imagens de duas câmeras para estimar a distância de objetos. As câmeras têm distância focal f (a distância entre o furo por onde passa a luz e o plano de imagens da câmera – o plano que contém os sensores das câmeras). Suponha que a lente no furo não mude a trajetória dos raios de luz. As câmeras foram colocadas lado a lado, com seus furos afastados por uma distância c, como indica a figura.
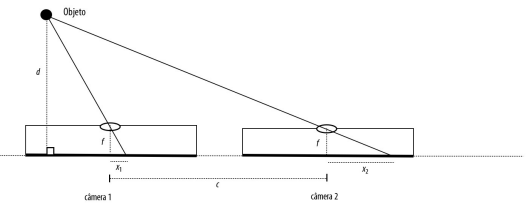
Certo objeto está a uma distância d do plano de imagens das câmeras (o plano que contém os sensores). Na imagem da câmera 1 (a da esquerda), o objeto aparece localizado em um pixel à direita do centro da imagem e a uma distância x1 deste centro. Já na imagem da câmera 2 (da direita), o objeto aparece localizado em um pixel também à direita do centro da imagem e a uma distância x2 deste centro, como mostra a figura.
a) Mostre que a distância d pode ser calculada em função de c, f, x1 e x2, por meio da expressão d = f ·
b)Se f e c são valores pequenos, da ordem de poucos centímetros, e o objeto está a uma distância d muito grande, como a lua ou uma estrela, o que podemos dizer sobre a relação entre x1 e x2?
a) Observe a figura a seguir:
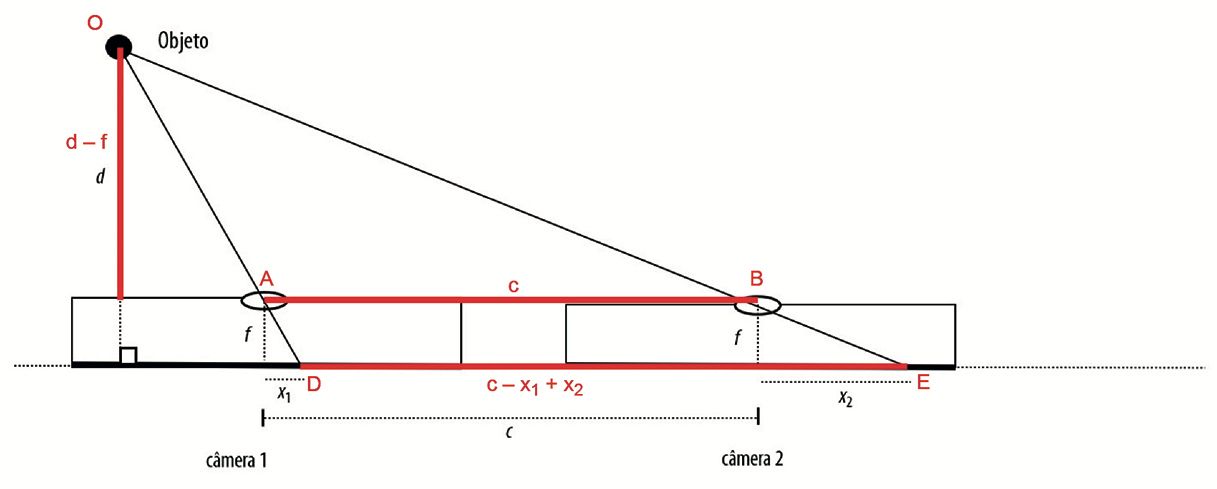
Da semelhança dos triângulos ODE e OAB, vem:
b) Do item anterior, tem-se a igualdade:
Como f é um valor pequeno e d é um valor muito grande, então . Com isso, tem-se
(pois é o resultado da divisão de um valor pequeno por um valor grande).
Logo, tem-se:
Isso significa que x2 está muito próximo de x1.