No sistema de coordenadas cartesianas, considere M pontos diferentes pertencentes ao semieixo positivo das abcissas e N pontos, também diferentes, pertencentes ao semieixo positivo das ordenadas.
Traçam-se os M × N segmentos de reta que unem cada um dos M pontos do semieixo das abcissas a cada um dos N pontos do semieixo das ordenadas.
Em cada uma das duas situações a seguir, calcule o número máximo de pontos de interseção desses M × N segmentos de reta que pertençam ao interior do primeiro quadrante, isto é, os pontos de interseção que tenham as duas coordenadas maiores do que zero:
a)M = N = 2.
b)M = 8 e N = 6.
a) Observe a figura a seguir:
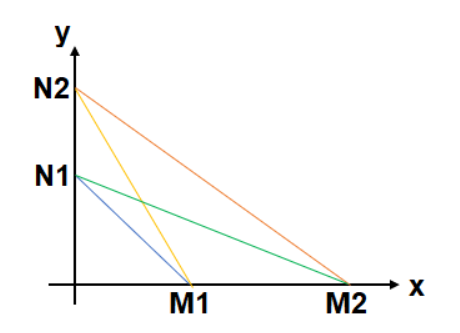
Com esses quatro segmentos, só há 1 ponto de intersecção entre dois deles que pertençam ao interior do primeiro quadrante (intersecção entre M1N2 e M2N1), pois nos demais casos, ou a intersecção é um ponto dos eixos coordenados ou não existe (M1N1 e M2N2).
b) Observe a figura a seguir:
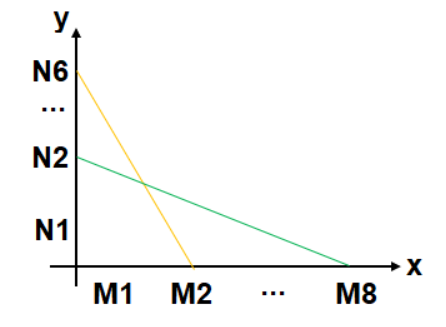
Escolhendo o ponto N1, tem-se que as interseções dos segmentos do conjunto {N1M1, N1M2, N1M3, ..., N1M8} são todos pertencentes ao eixo das ordenadas e nenhum deles está no interior do primeiro quadrante.
Escolhendo o ponto N2, tem-se:
- Existem 7 segmentos que intersectam N2M1 da forma N1Mx: N1M2, N1M3, N1M4, ..., N1M8;
- Existem 6 segmentos que intersectam N2M2 da forma N1Mx: N1M3, N1M4, N1M5, ..., N1M8;
- Existem 5 segmentos que intersectam N2M3 da forma N1Mx: N1M4, N1M5, N1M6, ..., N1M8;
- Existem 4 segmentos que intersectam N2M4 da forma N1Mx: N1M5, N1M6, N1M7, N1M8;
- Existem 3 segmentos que intersectam N2M5 da forma N1Mx: N1M6, N1M7, N1M8;
- Existem 2 segmentos que intersectam N2M6 da forma N1Mx: N1M7, N1M8;
- Existe 1 segmento que intersecta N2M7 da forma N1Mx: N1M8;
- Não existe segmento da forma N1Mx que intersecte N2M8.
Assim, esse total de intersecções é dado por 7 + 6 + 5 + 4 + 3 + 2 + 1 = 28.
Escolhendo o ponto N3, tem-se todos os 28 segmentos da forma N1Mx que intersectam N3Mx, bem como existem outros 28 segmentos da forma N2Mx que intersectam N3Mx, totalizando 2 · 28 intersecções.
Escolhendo o ponto N4, tem-se todos os 28 segmentos da forma N1Mx que intersectam N4Mx, bem como existem outros 28 segmentos da forma N2Mx que intersectam N4Mx e 28 segmentos da forma que intersectam N4Mx, totalizando 3 · 28 intersecções.
Escolhendo o ponto N5, tem-se todos os 28 segmentos da forma N1Mx que intersectam N5Mx, bem como existem outros 28 segmentos da forma N2Mx que intersectam N5Mx, 28 segmentos da forma N3Mx que intersectamN5Mx e 28 segmentos da forma N4Mx que intersectam N5Mx, totalizando 4 · 28 intersecções.
Por fim, escolhendo o ponto N6, tem-se todos os 28 segmentos da forma N1MX que intersectam N6MX, bem como existem outros 28 segmentos da forma N2MX que intersectam N6MX, 28 segmentos da forma N3MX que intersectam N6MX, 28 segmentos da forma N4MX que intersectam N6MX e 28 segmentos da forma N5MX que intersectam N6MX, totalizando 5 · 28 intersecções.
Logo, o total de intersecções é dado por 28 + 2 · 28 + 3 · 28 + 4 · 28 + 5 ·28 = 15 · 28 = 420.