Considere dois círculos concêntricos de centro O e raios diferentes.
Sejam AB um diâmetro do círculo maior e AC uma corda do círculo maior que é tangente ao círculo menor no ponto T.
O segmento BC mede 20 cm.
a) Faça uma figura que descreva a situação apresentada.
b) Calcule o raio do círculo menor.
a)
b)
Da figura construída no item anterior, temos:
- o segmento
, que é um raio da circunferência menor, é perpendicular ao segmento
, já que esse último é tangente à circunferência
- o triângulo ACB é retângulo em C, já que ele está inscrito na circunferência maior e seu lado
é um diâmetro da circunferência
A figura a seguir traz as observações feitas, denotando por r a medida do raio e por R as medidas dos raios
.
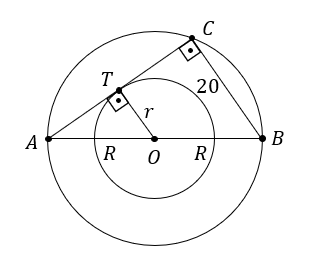
Como os triângulos retângulos ATO e ACB compartilham o ângulo de vértice em A, eles são semelhantes e, assim:
r = 10
Dessa forma, o raio do círculo menor mede 10 cm.