A curva da figura abaixo é chamada de espiral logarítmica. Todos os pontos (x, y) desta curva são tais que x = 2t · começar estilo tamanho matemático 14px cos espaço abre parênteses reto pi sobre 2 espaço vezes espaço reto t fecha parênteses espaço reto e espaço reto y espaço igual a espaço 2 à potência de reto t espaço vezes espaço sen espaço abre parênteses reto pi sobre 2 espaço vezes espaço reto t fecha parênteses vírgula fim do estilo para algum valor real t ≥ 0.

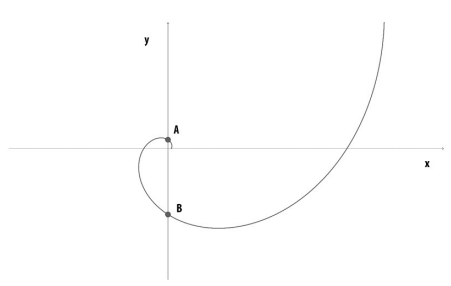
O ponto B é o ponto onde a curva intersecta a parte negativa do eixo Y com o menor valor de t possível. O valor da ordenada (coordenada Y) do ponto B é

  • a

    −8

  • b

    −1 

  • c

    −4 

  • d

    −16 

  • e

    −32

Para o ponto B, deve-se ter o menor valor positivo de t tal que x = 0 e y < 0, ou seja, o menor valor positivo de t, para o qual ocorre:

começar estilo tamanho matemático 14px abre chaves 2 à potência de reto t vezes cos abre parênteses reto pi sobre 2 reto t fecha parênteses igual a 0 2 à potência de reto t vezes sen abre parênteses reto pi sobre 2 reto t fecha parênteses menor que 0 fecha fim do estilo

Da primeira equação, vem 2t = 0 (não convém) ou começar estilo tamanho matemático 14px cos abre parênteses reto pi sobre 2 reto t fecha parênteses espaço igual a 0 fim do estilo. As primeiras soluções positivas da equação começar estilo tamanho matemático 14px cos abre parênteses reto pi sobre 2 reto t fecha parênteses espaço igual a 0 fim do estilo são começar estilo tamanho matemático 14px reto pi sobre 2 reto t igual a reto pi sobre 2 espaço ou espaço reto pi sobre 2 reto t igual a numerador 3 reto pi sobre denominador 2 fim da fração fim do estilo. 

Como começar estilo tamanho matemático 14px sen abre parênteses reto pi sobre 2 reto t fecha parênteses espaço menor que 0 fim do estilo, então deve-se ter começar estilo tamanho matemático 14px reto pi sobre 2 reto t igual a numerador 3 reto pi sobre denominador 2 fim da fração fim do estilo e, assim, t = 3. Portanto, a ordenada do ponto B é começar estilo tamanho matemático 14px 2 ao cubo vezes sen abre parênteses reto pi sobre 2 vezes 3 fecha parênteses igual a menos 8 fim do estilo.