A figura abaixo exibe um sólido formado por dois cubos idênticos, que compartilham uma aresta (como se fossem dois degraus de uma escada). As faces dos cubos que compartilham a aresta citada são perpendiculares. Estão destacados na figura os vértices A e B, cada um em um cubo. Sobre a superfície dos cubos, foi traçada a linha de menor comprimentoque liga o vértice A ao vértice B. Sabendo-se que os cubos têm aresta igual a 1, o comprimento da linha traçada é
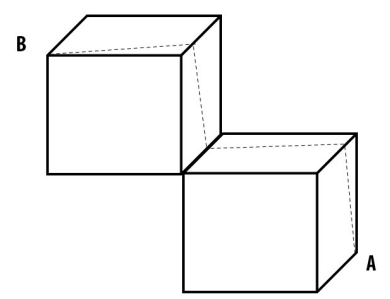
Observando na planificação somente as faces que contêm alguma parte da linha tracejada, obtém-se a figura a seguir:
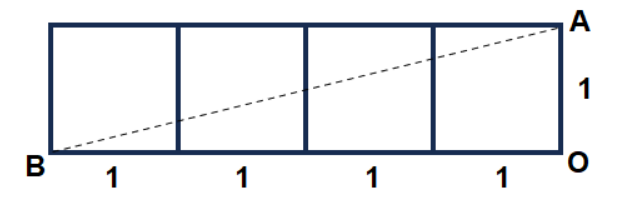
Aplicando o teorema de Pitágoras no triângulo retângulo AOB, tem-se: