Uma lista possui cinco números reais positivos e menores ou iguais a 10, podendo haver repetição. Nessa lista, existe apenas um número máximo, e a soma dos demais números é igual a 20.
a) Sendo M a média aritmética dos cinco números e x o maior deles, determine a expressão de M(x). Desenhe, no plano cartesiano presente no campo de Resolução e Resposta, o gráfico de M(x) e determine o domínio e a imagem dessa função.
b) Admita, agora, que a média, a mediana, a moda e a amplitude dos cinco números de tal lista sejam, respectivamente: 5,7; 7,0; 7,0 e 7,9. Determine os cinco números que compõem a lista.
a) Denotando os números por a, b, c, d e x, pode-se escrever o rol (a, b, c, d, x), com e cada um destes variando no intervalo ]0,10].
Além disso, do enunciado, tem-se que a + b + c + d = 20.
A média aritmética é dada por:
Agora:
1. Do enunciado, tem-se que e que
;
2. Dado que a + b + c + d = 20, então deve haver pelo menos um destes números que é maior ou igual a 5 (caso contrário, a soma a + b + c + d deveria ser menor que 20); como os números a, b, c e d estão em ordem crescente, então pelo menos ;
3. Como x é maior que todos esses números, então pode-se garantir que .
Desta forma, o domínio da função M(x) é o intervalo , sendo
um número real menor que 10 e que seja maior ou igual a 5 e maior ou igual a d.
Considerando que o domínio pedido seja o maior subconjunto possível nestas condições, então o domínio é dado pelo intervalo ]5,10] e, assim, é possível desenhar o gráfico de M(x):
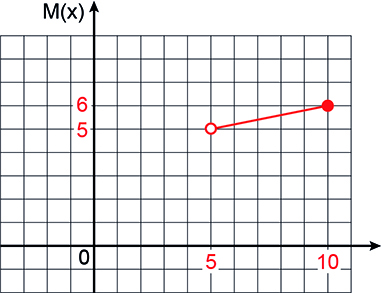
Com base no gráfico, conclui-se que o conjunto-imagem desta função é o intervalo ]5,6].
b) A partir do rol (a,b,c,d,x), tem-se:
- como a mediana vale 7, então c = 7;
- do item anterior, a média é dada por ; como esse valor é igual a 5,7, então
e, portanto, x = 8,5;
- como a amplitude vale 7,9, então x – a = 7,9 e, assim, a = 0,6;
- como a soma a + b + c + d = 20, então 0,6 + b + 7 + d = 20 e, portanto, b + d = 12,4; já que a moda vale 7, então b = 7 ou d = 7. Se b = 7, dado que b + d = 12,4, teríamos d = 5,4, o que é absurdo, pois b < d; então d = 7 e b = 5,4.
Portanto, deve-se ter a = 0,6; b = 5,4; c = 7; d = 7 e x = 8,5.