Em uma obra, uma caixa A é mantida em repouso no alto de uma prancha de madeira inclinada de um ângulo θ com a horizontal, com o auxílio de um sistema formado por duas polias e fios, todos ideais, e de um bloco B de massa 12 kg. A caixa A está inicialmente a 6,75 m de distância do ponto em que a prancha toca o solo (ponto S).
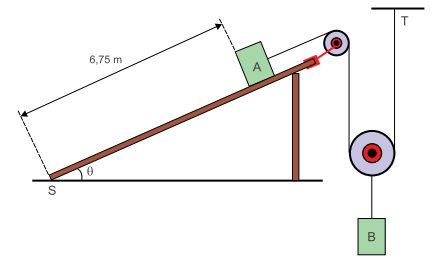
Desprezando os atritos e adotando g = 10 m/s2 e sen θ = 0,6, calcule:
a) o intervalo de tempo necessário, em segundos, para que a caixa A chegue ao ponto S, considerando que o fio que prende essa caixa se rompa.
b) a massa da caixa A, em kg, e a intensidade da força de tração, em N, que o fio ligado a essa caixa exerce no ponto em que ele está preso no teto (ponto T), na situação de equilíbrio mostrada na figura.
Depois que o fio se romper, as únicas forças aplicadas na caixa são a normal de contato e o peso, conforme ilustrado a seguir, com o peso já decomposto nas direções do plano e perpendicular ao plano.

Logo, como :
Substituindo-se os valores fornecidos:
Orientando-se a trajetória no mesmo sentido do movimento do corpo, podemos aplicar a equação dos espaços do MUV para determinar o tempo para a caixa chegar ao ponto S. Como ela parte do repouso:
b) Com o sistema em equilíbrio estático, temos os seguintes diagramas de corpo livre:
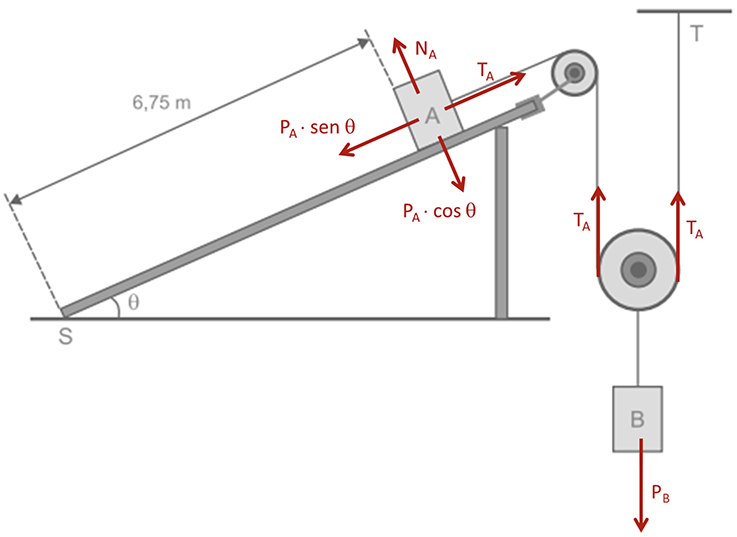
Equilíbrio da caixa A
Substituindo os valores numéricos fornecidos:
Equilíbrio da caixa B
Substituindo os valores numéricos fornecidos:
Substituindo (II) em (I):