A figura ilustra uma roda-gigante no exato instante em que a cadeira onde se encontra a pessoa P está no ponto mais alto dessa roda-gigante.
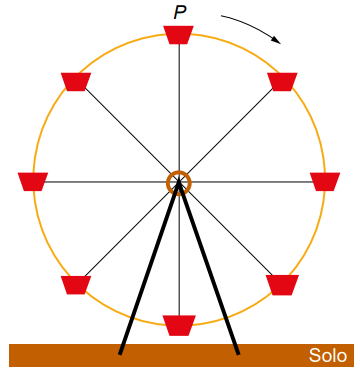
Com o passar do tempo, à medida que a roda-gigante gira, com velocidade angular constante e no sentido horário, a altura da cadeira onde se encontra a pessoa P, em relação ao solo, vai se alterando.
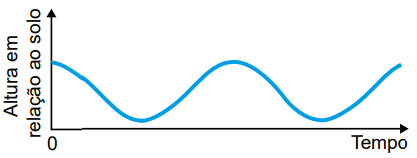
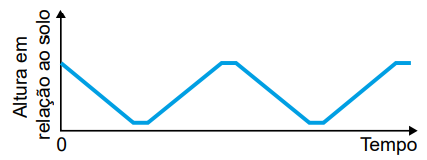
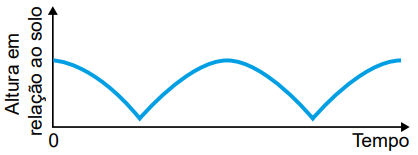
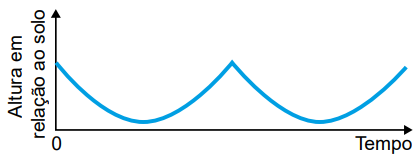
O gráfico que melhor representa a variação dessa altura, em função do tempo, contado a partir do instante em que a cadeira da pessoa P se encontra na posição mais alta da roda-gigante, é
Na figura a seguir, foi adotado um eixo y vertical com origem no solo.
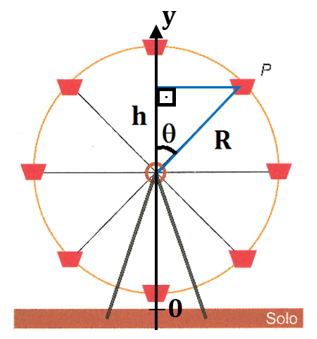
Seja R a medida do raio da circunferência que representa a roda-gigante e considere que o carrinho ocupa o ponto P representado, com o ângulo de medida tendo vértice no centro da circunferência e um dos lados sobre o eixo y. Temos, do triângulo retângulo formado:
Dessa forma, sendo H a altura do centro da roda-gigante em relação ao solo, a altura y da pessoa em relação ao solo é dada por:
Por fim, como a roda-gigante gira com velocidade angular ω constante, temos que, t segundos a partir do instante em que a pessoa se encontra na posição mais alta da roda-gigante, o arco θ tem medida ω⋅t, ou seja:
Trata-se, portanto, da lei de uma função trigonométrica. A única alternativa que exibe um gráfico desse tipo é A.
Observação: A rigor, a alternativa exibe o gráfico da altura em função do tempo, não de sua variação em função do tempo. Porém, entendemos que é possível visualizar a variação da altura a partir de sua própria medida.