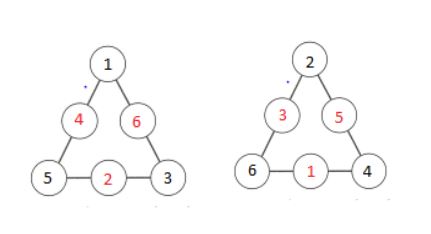
O triângulo da figura é denominado triângulo mágico. Nos círculos, escrevem-se os números de 1 a 6, sem repetição, com um número em cada círculo. O objetivo é distribuir os números de forma que as somas dos números em cada lado do triângulo sejam iguais.
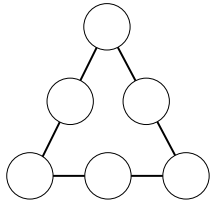
Considere que os números colocados nos vértices do triângulo estejam em progressão aritmética de razão igual a 2.
Nas condições propostas, quais as possíveis soluções para as somas dos números que formam os lados do triângulo?
Como os números dos vértices estão em progressão aritmética de razão 2, temos dois casos possíveis:
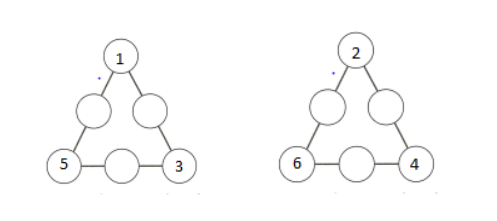
Para achar a soma ideal de cada lado, podemos somar todos os lados e dividir por três. Assim, as somas possíveis são:
Portanto, como as somas são 10 e 11, as únicas configurações possíveis são: