Uma equipe de segurança do transporte de uma empresa avalia o comportamento das tensões que aparecem em duas cordas, 1 e 2, usadas para prender uma carga de massa M = 200 kg na carroceria, conforme a ilustração. Quando o caminhão parte do repouso, sua aceleração é constante e igual a 3 m/s2 e, quando ele é freado bruscamente, sua frenagem é constante e igual a 5 m/s2. Em ambas as situações, a carga encontra-se na iminência de movimento, e o sentido do movimento do caminhão está indicado na figura. O coeficiente de atrito estático entre a caixa e o assoalho da carroceria é igual a 0,2. Considere a aceleração da gravidade igual a 10 m/s2, as tensões iniciais nas cordas iguais a zero e as duas cordas ideais.
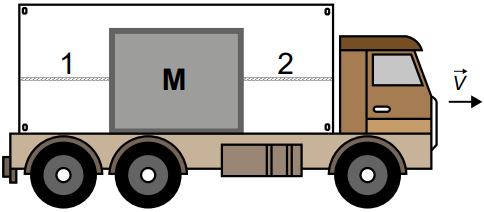
Nas situações de aceleração e frenagem do caminhão, as tensões nas cordas 1 e 2, em newton, serão
I) A figura seguinte ilustra as forças aplicadas na carga durante o intervalo de tempo em que o movimento do caminhão é acelerado:
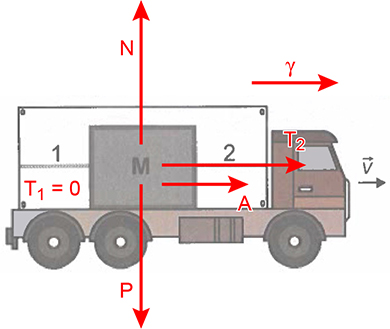
Note que, nessa situação, a tração no fio 1 é nula, ou seja, T1 = 0.
De acordo com o enunciado, durante esse movimento, a carga está na iminência de escorregamento, ou seja, o atrito nele aplicado é o estático máximo (). Além disso, como a carga está apoiada em uma superfície plana e horizontal, a normal e o peso se equilibram (N = P).
Aplicando o princípio fundamental da Dinâmica para essa situação:
Sendo μ = 0,2, m = 200 kg, g = 10 m/s2 e :
II) A figura seguinte ilustra as forças aplicadas na carga durante o intervalo de tempo em que o movimento do caminhão é retardado:
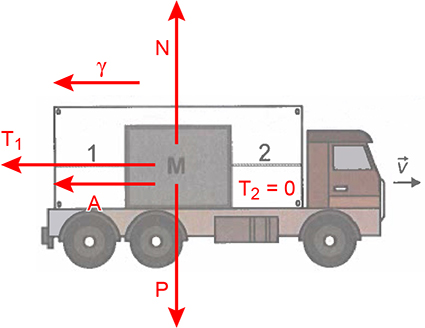
Note que, nessa situação, a tração no fio 2 é nula, ou seja, T2 = 0.
De acordo com o enunciado, durante esse movimento, a carga está na iminência de escorregamento, ou seja, o atrito nele aplicado é o estático máximo (). Além disso, como a carga está apoiada em uma superfície plana e horizontal, a normal e o peso se equilibram (N = P).
Aplicando o princípio fundamental da Dinâmica para essa situação:
Sendo μ = 0,2, m = 200 kg, g = 10 m/s2 e :