Laura é geóloga e está fazendo pesquisa numa caverna cuja entrada tem o formato de uma parábola invertida. Essa entrada, no nível do chão, tem 2m de largura e seu ponto mais alto está a 2,5m do chão, conforme figura a seguir.
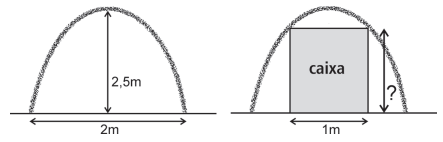
Para realizar sua pesquisa, ela precisa entrar na caverna com um equipamento guardado em uma caixa de 1m de largura. Qual é a altura máxima, em metros, que a caixa pode ter para passar pela entrada da caverna?
Podemos usar como modelo o arco de parábola, no plano xOy, dada por , com –1 ≤ x ≤ 1, em que a é uma constante negativa, tal que, para x = 0,
.
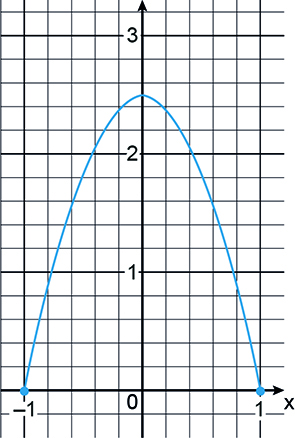
Substituindo x por 0 e y por , temos
, e, portanto,
Considerando , a altura máxima da caixa é dada por
.
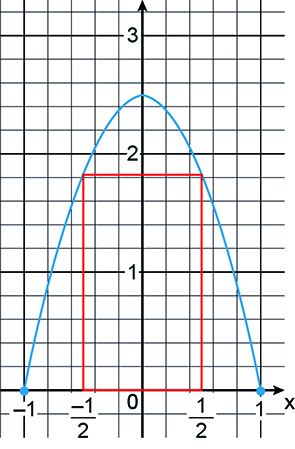
Temos