No plano cartesiano, a parábola de equação y = e a reta r de equação y = x + 3 se intersectam no ponto Q de coordenadas (0, 3), e no ponto P, como na figura.
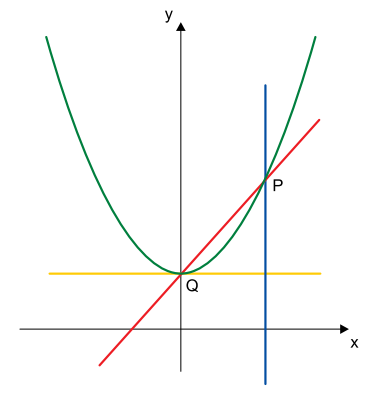
O triângulo delimitado pela reta r, pela reta horizontal que passa por Q e pela reta vertical que passa por P tem área
Inicialmente, vamos determinar as abscissas dos pontos de interseção P e Q:
Substituindo na equação , temos que a ordenada do ponto Q vale 3 e, a do ponto P, 7, de modo que o triângulo formado tem ambos os catetos medindo 4. Assim, sua área vale: