A figura mostra um raio de luz monocromática que se propaga no meio R, incide na superfície de uma lâmina de faces paralelas, constituída de um material S, sob ângulo de incidência δ, e penetra na lâmina. Em seguida, esse raio de luz incide na outra face da lâmina, a qual está em contato com um terceiro meio, T, onde sofre reflexão total.
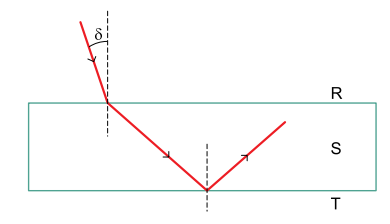
Considerando que sen δ = 0,60 e que o índice de refração absoluto do meio R é igual a 2,50, o máximo valor do índice de refração absoluto do meio T para que ocorra a reflexão total desse raio de luz na superfície entre S e T é
A geometria impõe que o ângulo de refração na fronteira R-S (ângulo β) tenha a mesma medida do ângulo de incidência na fronteira S- T, conforme ilustra a figura a seguir.
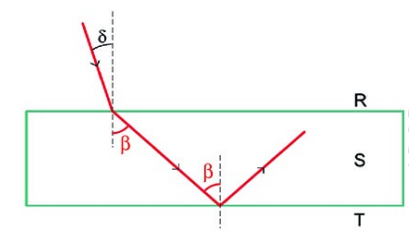
Aplicando a lei de Snell à primeira refração, tem-se:
Fazendo as devidas substituições numéricas:
Assim: (I)
Para que ocorra reflexão total na interface S-T, deve-se impor que o ângulo de incidência (β) seja maior que o ângulo limite (L) para esse par de meios.
Algebricamente:
β > L
Uma vez que esses ângulos pertencem ao primeiro quadrante trigonométrico, pode-se afirmar que:
sen β > sen L (II)
Em que: .
Uma vez que a reflexão total ocorre no interior do meio S, conclui-se que esse é o meio mais refringente. Assim sendo, nmaior = nS.
Segue então:
(III)
Substituindo as expressões I e III na expressão II, segue:
De onde se conclui que nT < 1,5.
Por se tratar de um intervalo aberto, não há sentido em se perguntar sobre o “máximo valor do índice de refração absoluto do meio T”.
Apesar da ressalva, pode-se inferir que valor pensado como resposta correta para essa questão seja o presente na alternativa D.