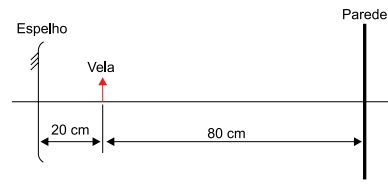
Ao ser colocado a 20 cm de uma vela acesa, um espelho côncavo projeta uma imagem nítida da chama da vela em uma parede situada a 80 cm da vela, como mostrado na figura.
a) Calcule a razão entre o tamanho da imagem da chama da vela e o tamanho dessa chama.
b) Sem deslocar a vela, retira-se o espelho e coloca-se uma lente delgada convergente entre a vela e a parede, de modo que nessa parede seja projetada uma imagem nítida da chama da vela com o triplo do tamanho da chama. Calcule a distância focal dessa lente, em centímetros.
a) A partir da figura, tem-se:
Distância do objeto ao espelho é 20 cm ⇒ p = 20 cm
Distância da imagem real (projetada) ao espelho é 100 cm ⇒ p’ = 100 cm
Usando a equação do aumento linear transversal (A), tomada em módulo, pode-se obter a razão entre o tamanho da imagem da chama da vela (y’) e o tamanho dessa chama (y).
Assim:
b) A figura a seguir ilustra a nova situação descrita.
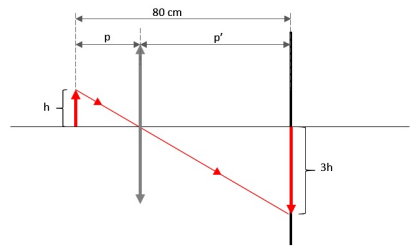
A partir da figura: p + p’ = 80 cm (equação I)
Por semelhança de triângulos:
(equação II)
Resolvendo o sistema de equações I e II têm-se: p = 20 cm e p’ = 60 cm.
Substituindo-se esses valores na equação de Gauss:
Segue que f = 15 cm, ou seja, a lente é do tipo convergente e sua distância focal vale 15 cm.