A figura representa uma mola de massa desprezível e constante elástica k = 20 N/m e comprimida de 20 cm. Uma das extremidades dessa mola está fixa em uma parede e na outra extremidade está preso um bloco que está apoiado em uma superfície horizontal e sem atrito.
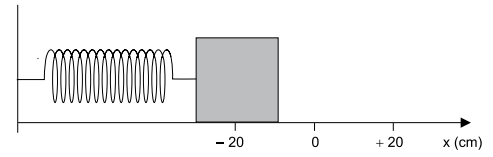
Em determinado instante, o bloco é liberado e passa a oscilar em movimento harmônico simples entre as posições x = – 20 cm e x = + 20 cm.
a) Sabendo que o intervalo de tempo para o bloco se deslocar da posição x = + 20 cm até a posição x = 0 cm é igual a 0,2 s, calcule o período de oscilação do sistema, em segundos, e a frequência de oscilação, em hertz.
b) Calcule a energia cinética do bloco, em joules, quando ele se encontra na posição x = + 10 cm.
a) O intervalo de tempo para o bloco se deslocar entre as elongações x = + 20 cm e x = 0 cm corresponde a do período sistema massa-mola, T. Assim:
Aplicando-se a relação entre a frequência e o período do movimento:
b) Como o sistema é conservativo:
Considerando que o plano horizontal de referência seja o plano em que o bloco se movimenta, a energia potencial gravitacional será sempre nula:
Considerando-se como situação inicial aquela em que o bloco está na elongação x = - 20 cm (deformação da mola igual a 20 cm e velocidade nula) e a posição final em que o bloco está na elongação igual a x = + 10 cm (deformação da mola igual a 10 cm),
Substituindo-se os valores, já ajustando as unidades adequadamente: