Ao se aproximar de um trecho em obras de uma rodovia, o motorista de um automóvel reduziu a velocidade, sem alteração da direção e de maneira uniforme, de 30 m/s para 20 m/s em um intervalo de tempo de 20 s.
a) Calcule o módulo da aceleração escalar produzida no automóvel, em m/s2, e a distância por ele percorrida, em metros, nesses 20 s.
b) Considerando que a massa do automóvel era de 800 kg, calcule a quantidade de movimento do automóvel, em kg·m/s, ao final da redução da velocidade e o módulo do impulso, em N·s, aplicado sobre o automóvel, no intervalo de tempo citado.
Representando a situação dada no enunciado:
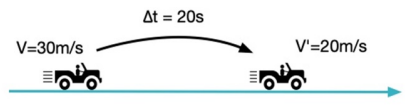
a) Aplicando a definição de aceleração escalar média:
Utilizando a equação de Torricelli:
b) A partir da definição de quantidade de movimento:
Considerando que o “impulso aplicado sobre o automóvel” seja o impulso da resultante no automóvel, podemos obtê-lo por meio do teorema do Impulso: